力扣刷题笔记
记录力扣刷题遇到的好题和优秀解法。部分题解来源于力扣对应题解,已注明出处。
1. 剑指 Offer 40. 最小的 k 个数
参考题解:4种解法秒杀 TopK (快排、堆、二叉搜索树 BST、计数排序)
这道题基于排序做十分简单。但是,由于只需要求最小的 k 个数,因此其实不用全部排序,只需要排序最小的 k 个即可。
因此,考虑做法:
1.1 快速排序
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if (k == 0 || arr.length == 0) {
return new int[0];
}
return quickSort(arr, 0, arr.length - 1, k - 1);
}
public int[] quickSort(int[] nums, int l, int h, int k) {
int j = partition(nums, l, h);
if (j == k) {
return Arrays.copyOf(nums, j + 1);
}
return j > k ? quickSort(nums, l, j - 1, k) : quickSort(nums, j + 1, h, k);
}
public int partition(int[] nums, int l, int h) {
int v = nums[l];
int i = l, j = h + 1;
while (true) {
while (++i <= h && nums[i] < v);
while (--j >= l && nums[j] > v);
if (i >= j) {
break;
}
int t = nums[j];
nums[j] = nums[i];
nums[i] = t;
}
nums[l] = nums[j];
nums[j] = v;
return j;
}
}1.2 堆
由于要求前 k 小,因此选择大根堆,每次把最大的 poll 出,从而让堆中元素最小。
这里是很有趣的逆向思维。一般我们要堆排序求最小,都是用小根堆。但那样的话,复杂度就是 O(nlogn),而不是 O(nlogk) 了。这里的逆向思维很妙。
基于 Java 提供的 PriorityQueue 可以快速实现。
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if (k == 0 || arr.length == 0) {
return new int[0];
}
Queue<Integer> pq = new PriorityQueue<>((v1, v2) -> v2 - v1);
for (int num: arr) {
if (pq.size() < k) {
pq.offer(num);
} else if (num < pq.peek()) {
pq.poll();
pq.offer(num);
}
}
int[] res = new int[pq.size()];
int idx = 0;
for (int num: pq) {
res[idx++] = num;
}
return res;
}
}1.3 二叉搜索树 BST
二叉搜索树求得的前 k 个值是有序的,因此是适合求 topK 问题的数据结构。
由于存在重复值,因此采用 TreeMap 实现更合适,而不是 TreeSet。
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if (k == 0 || arr.length == 0) {
return new int[0];
}
TreeMap<Integer, Integer> map = new TreeMap<>();
int cnt = 0;
for (int num: arr) {
if (cnt < k) {
map.put(num, map.getOrDefault(num, 0) + 1);
cnt++;
continue;
}
Map.Entry<Integer, Integer> entry = map.lastEntry();
if (entry.getKey() > num) {
map.put(num, map.getOrDefault(num, 0) + 1);
if (entry.getValue() == 1) {
map.pollLastEntry();
} else {
map.put(entry.getKey(), entry.getValue() - 1);
}
}
}
int[] res = new int[k];
int idx = 0;
for (Map.Entry<Integer, Integer> entry: map.entrySet()) {
int freq = entry.getValue();
while (freq-- > 0) {
res[idx++] = entry.getKey();
}
}
return res;
}
}1.4 计数排序
当数据量比较小时,可以直接采用计数排序。
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if (k == 0 || arr.length == 0) {
return new int[0];
}
int[] counter = new int[10001];
for (int num: arr) {
counter[num]++;
}
int[] res = new int[k];
int idx = 0;
for (int num = 0; num < counter.length; num++) {
while (counter[num]-- > 0 && idx < k) {
res[idx++] = num;
}
if (idx == k) {
break;
}
}
return res;
}
}2. 第 84 题. 柱状图中最大的矩形
参考题解:单调栈入门,使用单调栈快速寻找边界
这道题可以分为两种思路:
- 限定高度。
- 限定宽度。
其中,限定宽度的复杂度是 O(n^2),限定高度复杂度是 O(n),因此选择,固定每个柱的高度,向左右延伸,看看有没有比最大值还要大的矩形。
单调栈是一种很适合这里的数据结构,如果新的元素比栈顶元素大,入栈。如果比栈顶元素小,就一个个弹出,直到栈没有元素或者新元素比栈顶元素大。
- 元素出栈时,说明
新元素是出栈元素向后找第一个比其小的元素。 - 元素出栈后,说明
新栈顶元素是出栈元素向前找第一个比其小的元素。

代码模板如下:
Stack<Integer> s = new Stack<>();
for (int i = 0; i < height.length; ++i) {
while (!s.isEmpty() && height[s.peek()] > height[i]) {
s.pop();
}
s.push(i);
}对应于这道题,就要在出栈时进行计算,以比较矩阵大小。
代码如下:
class Solution {
public int largestRectangleArea(int[] heights) {
Integer ans = 0;
int[] height = new int[heights.length + 2];
height[0] = 0;
height[height.length - 1] = 0;
for (int i = 1; i < height.length - 1; ++i) {
height[i] = heights[i - 1];
}
Stack<Integer> s = new Stack<>();
for (int i = 0; i < height.length; ++i) {
while (!s.isEmpty() && height[s.peek()] > height[i]) {
int cur = s.pop();
int left = s.peek() + 1;
int right = i - 1;
Integer temp = (right - left + 1) * height[cur];
ans = temp.compareTo(ans) == 1 ? temp : ans;
}
s.push(i);
}
return ans;
}
}3. 买卖股票的最佳时期
3.4 增加 k 笔交易限制
参考题解:Java 动态规划 清晰简明
这道题的思路包括:
-
数组由二维变换为三维,其中第三个维度是交易限制。
-
由于交易限制 k 可能比天数 n 的一半大,所以交易限制要和 n / 2 比较一下,如果超过了 n / 2,限制就要变成 n / 2了。
-
初始状态是:i = 0 时,购买第 0 件商品,带来花费。
-
状态转移方程,要首先和交易限制进行比较,判断能不能卖出。
-
买入和卖出都是当天的价格,所以 + - prices[i]。
-
卖出了算完成一次交易,所以
dp[i - 1][1][j + 1] + prices[i],而dp[i - 1][0][j] - prices[i],前面卖出完成交易,所以j + 1,而后面买入,j不发生改变。
class Solution {
public int maxProfit(int k, int[] prices) {
int n = prices.length;
if (n == 0) {
return 0;
}
k = Math.min(k, n / 2);
int[][][] dp = new int[n][2][k + 1];
for (int i = 0; i <= k; ++i) {
dp[0][1][i] = -prices[0];
}
for (int i = 1; i < n; ++i) {
for (int j = 0; j <= k; ++j) {
if (j < k) {
dp[i][0][j] = Math.max(dp[i - 1][0][j], dp[i - 1][1][j + 1] + prices[i]);
} else {
dp[i][0][j] = dp[i - 1][0][j];
}
dp[i][1][j] = Math.max(dp[i - 1][1][j], dp[i - 1][0][j] - prices[i]);
}
}
int res = 0;
for (int i = 0; i <= k; ++i) {
res = Math.max(res, dp[n - 1][0][i]);
}
return res;
}
}4. 剑指 Offer 07. 重建二叉树
参考题解:二叉树的前序遍历 (分支思想)
这道题的思路包括:
- 根据前序遍历和中序遍历,可以很轻易看出,前序遍历可以获取根节点,然后将中序遍历划分为两个子区间,这是一个清晰的分治问题。
- 但是,如何根据前序遍历数组,将两个遍历数组联系起来,这就需要通过 HashMap 存储每个前序遍历节点的位置。
- 随后,建树函数需要存储前序遍历和中序遍历分别对应的数组中的起始和终止的位置。
- 最后,分治时的子树的左右节点,对应的前序、中序遍历的起始、终止位置,这里需要记忆一下。可以分别记忆前序和中序的内容,因为都是两两对应的。
public class Solution {
private Map<Integer, Integer> reverses;
private int[] preorder;
public TreeNode buildTree(int[] preorder, int[] inorder) {
int preLen = preorder.length;
int inLen = inorder.length;
if (preLen != inLen) {
return null;
}
this.preorder = preorder;
reverses = new HashMap<>(inLen);
for (int i = 0; i < inLen; i++) {
reverses.put(inorder[i], i);
}
return buildTree(0, preLen - 1, 0, inLen - 1);
}
private TreeNode buildTree(int preL, int preR, int inL, int inR) {
if (preL > preR || inL > inR) {
return null;
}
int pivot = preorder[preL];
TreeNode root = new TreeNode(pivot);
int pivotIndex = reverses.get(pivot);
root.left = buildTree(preL + 1, preL + (pivotIndex - inL), inL, pivotIndex - 1);
root.right = buildTree(preL + (pivotIndex - inL) + 1, preR, pivotIndex + 1, inR);
return root;
}
}5. 第86题 分割链表
个人题解:双指针法 超过100%
这道题的思路包括:
-
可以采用构建两个链表,一大一小,最后合并的方式实现小元素在大元素之前。
-
个人认为还是原链表上修改更锻炼算法能力,采用双指针法实现更优。
-
构建带有头结点的双指针,可以更好遍历。
-
基于各个指针的 next 进行比较和判断。
-
首先找到大指针对应的元素,随后在 while 循环中找到小指针对应的元素。
-
注意,需要设定 flag,以保证小指针是在大指针后面找到的,从而避免交换错位。
-
交换步骤需要经过三次指针调整。
-
交换之后,大指针需要前进一位,因为前面的元素多了一位。
class Solution {
public ListNode partition(ListNode head, int x) {
ListNode temp1 = new ListNode(0), temp2 = temp1, res = temp1;
temp1.next = head;
boolean flag = false;
while (temp2.next != null && temp2.next.val < x) {
temp2 = temp2.next;
}
if (temp2.next == null) {
return res.next;
}
while (true) {
while (temp1.next != null && temp1.next.val >= x) {
flag = true;
temp1 = temp1.next;
continue;
}
if (temp1.next == null) {
return res.next;
}
if (flag == false) {
temp1 = temp1.next;
continue;
}
/*
这里很关键,如果不设置这个flag,就会造成前面的部分被“吃掉”。
必须要保证temp2在temp1前面,这样才是逆序,才可以交换。
*/
ListNode temp3 = temp1.next;
temp1.next = temp1.next.next;
temp3.next = temp2.next;
temp2.next = temp3;
temp2 = temp2.next;
if (temp1.next == null) {
return res.next;
}
}
}
}6. 剑指 offer 11. 旋转数组的最小数字
个人题解:二分搜索求解旋转数组最小数
这道题的思路包括:
- 这道题可以用三个判断实现求解。
- 如果中位数比右边小,说明最小数在左边。
- 如果中位数比右边大,说明最小数在右边。
- 如果中位数和右边相等,说明答案在中间,这时候应该让右边向左移动一位!
- 根据二分搜索模板,最后返回 left 指向的元素。
class Solution {
public int minArray(int[] numbers) {
int left = 0, right = numbers.length - 1, mid = 0;
while (left < right) {
mid = (left + right) >> 1;
if (numbers[mid] < numbers[right]) {
right = mid;
} else if (numbers[mid] > numbers[right]) {
left = mid + 1;
} else {
right -= 1;
}
}
return numbers[left];
}
}7. 剑指 offer 12. 矩阵中的路径
参考题解:矩阵中的路径 DFS + 剪枝
这道题的思路包括:
- 这道题是最标准的深度优先搜索回溯问题。
- 同时,这道题非常经典,要求了不能重复走。
- Java 解回溯最好还是用递归。我一开始用了迭代,后来发现,Java 没有办法将不同类型的元素放在一个栈中,因此没有办法在栈中放入重复走判断矩阵,只能用递归。
- 递归可以临时修改 board,递归结束时再改回来,这样可以省去判断矩阵的空间。
class Solution {
public boolean exist(char[][] board, String word) {
char[] words = word.toCharArray();
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
if (dfs(board, words, i, j, 0)) return true;
}
}
return false;
}
boolean dfs(char[][] board, char[] word, int i, int j, int k) {
if(i >= board.length || i < 0 || j >= board[0].length || j < 0 || board[i][j] != word[k]) return false;
if(k == word.length - 1) return true;
board[i][j] = '\0';
boolean res = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1) ||
dfs(board, word, i, j + 1, k + 1) || dfs(board, word, i , j - 1, k + 1);
board[i][j] = word[k];
return res;
}
}8. 第 399 题. 除法求值
参考题解:除法求值
这道题的思路包括:
- 这道题很清晰的是并查集的题目。
- 除了简单的路径压缩,这道题还涉及权值合并,因此较为复杂。
- 实现起来有一些难度,这道题给了 Java 求解带权并查集的模板。
import java.util.HashMap;
import java.util.List;
import java.util.Map;
public class Solution {
public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
int equationsSize = equations.size();
UnionFind unionFind = new UnionFind(2 * equationsSize);
// 第 1 步:预处理,将变量的值与 id 进行映射,使得并查集的底层使用数组实现,方便编码
Map<String, Integer> hashMap = new HashMap<>(2 * equationsSize);
int id = 0;
for (int i = 0; i < equationsSize; i++) {
List<String> equation = equations.get(i);
String var1 = equation.get(0);
String var2 = equation.get(1);
if (!hashMap.containsKey(var1)) {
hashMap.put(var1, id);
id++;
}
if (!hashMap.containsKey(var2)) {
hashMap.put(var2, id);
id++;
}
unionFind.union(hashMap.get(var1), hashMap.get(var2), values[i]);
}
// 第 2 步:做查询
int queriesSize = queries.size();
double[] res = new double[queriesSize];
for (int i = 0; i < queriesSize; i++) {
String var1 = queries.get(i).get(0);
String var2 = queries.get(i).get(1);
Integer id1 = hashMap.get(var1);
Integer id2 = hashMap.get(var2);
if (id1 == null || id2 == null) {
res[i] = -1.0d;
} else {
res[i] = unionFind.isConected(id1, id2);
}
}
return res;
}
private class UnionFind {
private int[] parent;
private double[] weight;
public UnionFind(int n) {
this.parent = new int[n];
this.weight = new double[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
weight[i] = 1.0d;
}
}
public void union(int x, int y, double value) {
int rootX = find(x);
int rootY = find(y);
if (rootX == rootY) {
return;
}
parent[rootX] = rootY;
weight[rootX] = weight[y] * value / weight[x];
}
public int find(int x) {
if (x != parent[x]) {
int origin = parent[x];
parent[x] = find(parent[x]);
weight[x] *= weight[origin];
}
return parent[x];
}
public double isConected(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX == rootY) {
return weight[x] / weight[y];
} else {
return -1.0d;
}
}
}
}9. 第547题. 省份数量
个人题解:Java 并查集 求解问题
这道题的思路包括:
- 采用并查集求解问题。
- 与第399题类似,但没有权值了,相对而言更加简单一些。
- 需要判断根节点数量。利用了并查集性质:i == parent[i] 则为根节点。
class Solution {
private class UnionFind {
private int[] parent;
public UnionFind(int n) {
this.parent = new int[n];
for (int i = 0; i < n; ++i) {
parent[i] = i;
}
}
public void union(int x, int y) {
int rootx = find(x);
int rooty = find(y);
if (rootx != rooty) {
parent[rootx] = rooty;
}
}
public int result() {
// 用于返回最终结果
int count = 0;
for (int i = 0; i < parent.length; ++i) {
if (i == parent[i]) {
count++;
}
}
return count;
}
public int find(int x) {
if (x != parent[x]) {
parent[x] = find(parent[x]);
}
return parent[x];
}
}
public int findCircleNum(int[][] isConnected) {
int n = isConnected.length, count = 0;
UnionFind u = new UnionFind(n);
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
if (isConnected[i][j] == 1) {
u.union(i, j);
}
}
}
return u.result();
}
}10. 第189题. 旋转数组
参考题解:旋转数组
这道题非常经典,要求是将数组的所有值后移 k 位。要求尽量用空间复杂度为 O(1) 的算法。
因此,考虑方法:
10.1 额外数组
最简单的方法,直接新建一个一样大的数组,存储移动后的对应元素即可。
10.2 环形替换法
环形替换法是最老老实实的方法,思想也很巧妙,时间复杂度是最低的,空间复杂度 O(1)。
这种方法的思想包括:
- 迭代数组中的每一个位置,作为起始点位置。
- 从起始点位置开始,进行自循环,后移交换后面第 k 位的元素,直到回到起始点的位置,结束子循环。
- 利用 count 计数,表示已经完成交换的元素数量。当 count == n 时,返回。
class Solution {
public void rotate(int[] nums, int k) {
int n = nums.length;
k = k % n;
int count = 0;
for (int start = 0; start < n; ++start) {
int current = start;
int prev = nums[start];
do {
int next = (current + k) % n;
int temp = nums[next];
nums[next] = prev;
prev = temp;
current = next;
count++;
if (count == n) {
return;
}
} while (start != current);
}
}
}10.3 数组旋转法
数组旋转法是空间复杂度为 O(1) 且时间复杂度为 O(n) 的方法,并且十分好写,推荐用这种方法。
这种方法的思路包括:
- 先对数组整体旋转,将后面 k 位挪到前面来。
- 分别对前面 k 位和后面 n - k 位进行旋转,即可获得最终数组。
class Solution {
public void rotate(int[] nums, int k) {
k %= nums.length;
reverse(nums, 0, nums.length - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, nums.length - 1);
}
private void reverse(int[] nums, int start, int end) {
while (start < end) {
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start++;
end--;
}
}
} 11. 第1202题. 交换字符串中的元素
参考题解:Java 59 ms 并查集
这道题的思路包括:
- 这道题提供了可以交换位置的列表,这是涉及到连通性的问题。
- 遇到连通性问题,首先考虑并查集、图论。
- 这道题使用了并查集。
- 根据列表,获取并查集。
- 将并查集内元素排序,从而获得最小字典序字符串。
- 排序使用了 HashMap 和 PriorityQueue,分别用来存储并查集根节点号和字符。
- 最后进行一次遍历,获取 HashMap 的 PriorityQueue 中调用 find 函数找到的并查集的头结点,即可获取对应字典序最小的字符。
- 使用 StringBuilder 即可完成最终字符串的合并。
class Solution {
private class UnionFind {
private int[] parent;
public UnionFind(int n) {
this.parent = new int[n];
for (int i = 0; i < n; ++i) {
parent[i] = i;
}
}
public void union(int x, int y) {
int rootx = find(x);
int rooty = find(y);
if (rootx != rooty) {
parent[rootx] = rooty;
}
}
public int find(int x) {
if (x != parent[x]) {
parent[x] = find(parent[x]);
}
return parent[x];
}
}
public String smallestStringWithSwaps(String s, List<List<Integer>> pairs) {
char[] c = s.toCharArray();
int n = s.length();
UnionFind u = new UnionFind(n);
for (int i = 0; i < pairs.size(); ++i) {
int a = pairs.get(i).get(0), b = pairs.get(i).get(1);
u.union(a, b);
}
StringBuilder sb = new StringBuilder();
HashMap<Integer, PriorityQueue<Character>> map = new HashMap<>();
for (int i = 0; i < s.length(); i++) {
int r = u.find(i);
if (map.get(r) == null){
int finalI = i;
map.put(r,new PriorityQueue<Character>(){{offer(s.charAt(finalI));}});
} else {
map.get(r).offer(s.charAt(i));
}
}
for (int i = 0; i < s.length(); i++) {
Character poll = map.get(u.find(i)).poll();
if (poll!=null) sb.append(poll);
}
return sb.toString();
}
}12. 第1584题. 连接所有点的最小费用
个人题解:Kruskal 求解问题
这道题的思路包括:
-
看到所有边都有路径,最短总路径,马上想到 Kruskal。
-
Kruskal 用到的是并查集,需要并查集类;还需要对边排序,需要边类。
-
需要求所有点之间的距离,放到 List\
arrayListA 内,随后对其进行排序。 -
排序写法:
-
Collections.sort(arrayListA, new Comparator() { public int compare(Edge e1, Edge e2) { return e1.weight - e2.weight; } });
class Solution {
public class UnionFind {
private int[] parent;
public UnionFind(int n) {
parent = new int[n];
for (int i = 0; i < n; ++i) {
parent[i] = i;
}
}
public boolean union(int x, int y) {
int rootx = find(x);
int rooty = find(y);
if (rootx != rooty) {
parent[rootx] = rooty;
return true;
}
return false;
}
public int find(int x) {
if (x != parent[x]) {
parent[x] = find(parent[x]);
}
return parent[x];
}
}
public class Edge {
private int x, y, weight;
public Edge(int weight, int x, int y) {
this.x = x;
this.y = y;
this.weight = weight;
}
}
public int minCostConnectPoints(int[][] points) {
int n = points.length;
UnionFind u = new UnionFind(n);
List<Edge> l = new ArrayList<>();
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
l.add(new Edge(getDistance(points, i, j), i, j));
}
}
Collections.sort(l, new Comparator<Edge>() {
public int compare(Edge e1, Edge e2) {
return e1.weight - e2.weight;
}
});
int res = 0, num = 1;
for (Edge e : l) {
int weight = e.weight, x = e.x, y = e.y;
if (u.union(x, y)) {
res += weight;
num++;
if (num == n) {
break;
}
}
}
return res;
}
public int getDistance(int[][] points, int x, int y) {
return Math.abs(points[x][0] - points[y][0]) + Math.abs(points[x][1] - points[y][1]);
}
}13. 第1319题. 连通网络的操作次数
参考题解:连通网络的操作次数
这道题的思路包括:
- 这道题是连通网络题,很明显考察的是并查集。
- 这道题是并查集的一个变种,需要加入 size 来判断 rootx 和 rooty 哪个更常用,并将常用的作为根节点。
- 同时,最开始需要判断 length 和 n - 1,否则结果还是有问题。
class Solution {
public class UnionFind {
private int[] parent;
private int[] size;
private int count;
private int num;
public UnionFind(int n) {
count = n - 1;
num = n;
parent = new int[n];
size = new int[n];
for (int i = 0; i < n; ++i) {
parent[i] = i;
size[i] = 1;
}
}
public void union(int x, int y) {
int rootx = find(x);
int rooty = find(y);
if (rootx != rooty) {
if (size[rootx] <= size[rooty]) {
parent[rootx] = rooty;
size[rooty] += size[rootx];
} else {
parent[rooty] = rootx;
size[rootx] += size[rooty];
}
count--;
}
}
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
public int getResult() {
return count >= 0 ? count : -1;
}
}
public int makeConnected(int n, int[][] connections) {
if (connections.length < n - 1) {
return -1;
}
UnionFind u = new UnionFind(n);
for (int i = 0; i < connections.length; ++i) {
u.union(connections[i][0], connections[i][1]);
}
return u.getResult();
}
}14. 第959题. 由斜杠划分区域
参考题解:由斜杠划分区域
这道题的思路包括:
- 这道题看似比较困难,但如果能将它建模成并查集问题,就可以迎刃而解了。


- 可以看到,将每个格划分为四个部分,根据需要合并内部和外部的对应部分。
- 设置 count = n,每合并一次减少一点 count,最后返回 count 即可。
class Solution {
public class UnionFind {
private int[] parent;
private int count;
public UnionFind(int n) {
count = n;
parent = new int[n];
for (int i = 0; i < n; ++i) {
parent[i] = i;
}
}
public int getResult() {
return count;
}
public void union(int x, int y) {
int rootx = find(x);
int rooty = find(y);
if (rootx != rooty) {
parent[rootx] = rooty;
count--;
}
}
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
}
public int regionsBySlashes(String[] grid) {
int n = grid.length;
int size = 4 * n * n;
UnionFind u = new UnionFind(size);
for (int i = 0; i < n; ++i) {
char[] row = grid[i].toCharArray();
for (int j = 0; j < n; ++j) {
int index = 4 * (i * n + j);
char c = row[j];
if (c == '/') {
u.union(index, index + 3);
u.union(index + 1, index + 2);
} else if (c == '\\') {
u.union(index, index + 1);
u.union(index + 2, index + 3);
} else {
u.union(index, index + 1);
u.union(index + 1, index + 2);
u.union(index + 2, index + 3);
}
if (j + 1 < n) {
u.union(index + 1, 4 * (i * n + j + 1) + 3);
}
if (i + 1 < n) {
u.union(index + 2, 4 * ((i + 1) * n + j));
}
}
}
return u.getResult();
}
}15. 第1631题. 最小体力消耗路径
参考题解:最小体力消耗路径
这道题有三种解法:
15.1 二分查找法
二分查找法的思路主要包括:
-
目标是找到使路径可以通行的最小距离差,因此,可以通过二分法求解。
-
设置最小值和最大值,目标是使 dist < ans 时无法通过, dist >= ans 时可以通过。
-
判断是否能够通过可以基于深度优先搜索实现。
class Solution {
public int minimumEffortPath(int[][] heights) {
int[][] dir = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int m = heights.length, n = heights[0].length, left = 0, right = 999999, ans = 0;
while (left <= right) {
int mid = (left + right) >> 1;
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{0, 0});
boolean[] seen = new boolean[m * n];
seen[0] = true;
while (!queue.isEmpty()) {
int[] cell = queue.poll();
int x = cell[0], y = cell[1];
for (int i = 0; i < 4; ++i) {
int nx = x + dir[i][0], ny = y + dir[i][1];
if (nx >= 0 && nx < m && ny >= 0 && ny < n && !seen[nx * n + ny] && Math.abs(heights[x][y] - heights[nx][ny]) <= mid) {
queue.offer(new int[]{nx, ny});
seen[nx * n + ny] = true;
}
}
}
if (seen[m * n - 1]) {
ans = mid;
right = mid - 1;
} else {
left = mid + 1;
}
}
return ans;
}
}15.2 并查集法
并查集法的思路主要包括:
- 由于这道题对距离定义的特殊性,也就是路径总距离并不考虑有多少条边,而只考虑最长的一条边,因此可以对所有边排序,慢慢加入最小的边,直到左下和右上连同为止。
- 这样建模后,就可以使用并查集思想求解了。
class Solution {
public int minimumEffortPath(int[][] heights) {
int m = heights.length, n = heights[0].length;
List<int[]> edges = new ArrayList<int[]>();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
int id = i * n + j;
if (i > 0) {
edges.add(new int[]{id - n, id, Math.abs(heights[i][j] - heights[i - 1][j])});
}
if (j > 0) {
edges.add(new int[]{id - 1, id, Math.abs(heights[i][j] - heights[i][j - 1])});
}
}
}
Collections.sort(edges, new Comparator<int[]>() {
public int compare(int[] edge1, int[] edge2) {
return edge1[2] - edge2[2];
}
});
UnionFind uf = new UnionFind(m * n);
int ans = 0;
for (int[] edge : edges) {
int x = edge[0], y = edge[1], v = edge[2];
uf.unite(x, y);
if (uf.connected(0, m * n - 1)) {
ans = v;
break;
}
}
return ans;
}
}
class UnionFind {
int[] parent;
int[] size;
int n;
// 当前连通分量数目
int setCount;
public UnionFind(int n) {
this.n = n;
this.setCount = n;
this.parent = new int[n];
this.size = new int[n];
Arrays.fill(size, 1);
for (int i = 0; i < n; ++i) {
parent[i] = i;
}
}
public int findset(int x) {
return parent[x] == x ? x : (parent[x] = findset(parent[x]));
}
public boolean unite(int x, int y) {
x = findset(x);
y = findset(y);
if (x == y) {
return false;
}
if (size[x] < size[y]) {
int temp = x;
x = y;
y = temp;
}
parent[y] = x;
size[x] += size[y];
--setCount;
return true;
}
public boolean connected(int x, int y) {
x = findset(x);
y = findset(y);
return x == y;
}
}15.3 Dijkstra 法
Dijkstra 法的思路主要包括:
- 由于要求解的问题属于单源最短路径问题,因此很适合 Dijkstra 算法。
- 题目定义的距离稍有不同,简单进行改动即可,即一条路径的距离是这条路径上最大的权值差值。
class Solution {
public int minimumEffortPath(int[][] heights) {
int[][] dir = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int m = heights.length, n = heights[0].length;
PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {
public int compare(int[] edge1, int[] edge2) {
return edge1[2] - edge2[2];
}
});
pq.offer(new int[]{0, 0, 0});
int[] dist = new int[m * n];
Arrays.fill(dist, Integer.MAX_VALUE);
dist[0] = 0;
boolean[] seen = new boolean[m * n];
while (!pq.isEmpty()) {
int[] edge = pq.poll();
int x = edge[0], y = edge[1], d = edge[2];
int id = x * n + y;
if (seen[id]) {
continue;
}
if (x == m - 1 && y == n - 1) {
break;
}
seen[id] = true;
for (int i = 0; i < 4; ++i) {
int nx = x + dir[i][0], ny = y + dir[i][1];
if (nx >= 0 && nx < m && ny >= 0 && ny < n) {
int temp = Math.max(d, Math.abs(heights[x][y] - heights[nx][ny]));
if (temp < dist[nx * n + ny]) {
dist[nx * n + ny] = temp;
pq.offer(new int[]{nx, ny, dist[nx * n + ny]});
}
}
}
}
return dist[m * n - 1];
}
}16. 第 424 题. 替换后的最长重复字符
参考题解:替换后的最长重复字符
这道题的思路包括:
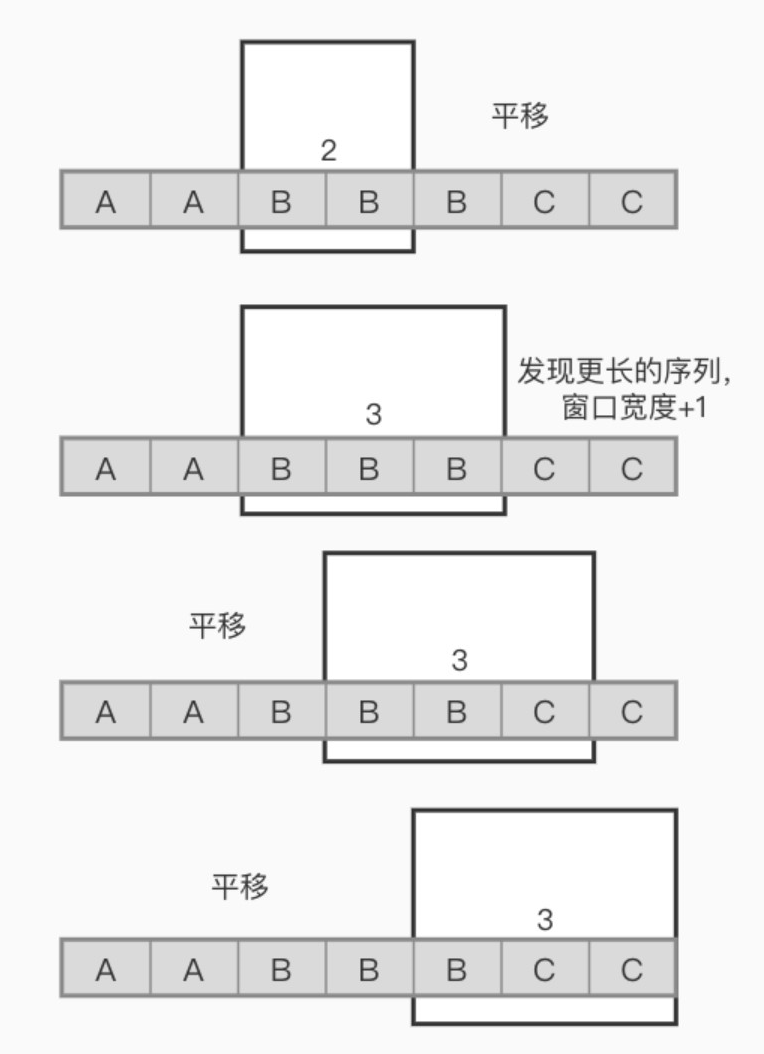
- 这道题用动态规划不好做,用双指针法是比较好做的。
- 可以建一个数组,存储每个字母在两个指针间的数量。
- 右指针遍历每个元素,并对指向的字母进行数据更新。
- 存储最大数量。如果两指针间距减去最大数量超过 k,说明左指针应该右移一次了,同时左指针指向的数据更新。
- 为什么只移动一格呢?为了保证指针间距不变,不会影响到最终答案。
- 这道题还是比较难思考的,主要是左指针最多一次只能移动一格那里,比较难思考。
class Solution {
public int characterReplacement(String s, int k) {
int[] num = new int[26];
int n = s.length();
int maxn = 0;
int left = 0, right = 0;
while (right < n) {
num[s.charAt(right) - 'A']++;
maxn = Math.max(maxn, num[s.charAt(right) - 'A']);
if (right - left + 1 - maxn > k) {
num[s.charAt(left) - 'A']--;
left++;
}
right++;
}
return right - left;
}
}17. 第 338 题. 比特位计数
参考题解:清晰的思路
这道题的思路包括:
-
这道题一看就是动态规划,规律需要记一下,估计是以后面试会常考的题。
-
初始条件:0 的 1 个数是 0。
-
奇数的 1 的个数,一定比前面的数多一个 1,多的就是最低位的 1。
-
偶数的 1 的个数,和除以二的数一样多,因为最低位都是0,除以 2 就是右移一位,1 的个数不变。
-

18. 第 503 题. 下一个更大元素 II
参考题解:Java 动态规划 双百
这道题的思路包括:
- 可以基于动态规划做。通过动态规划,缩减重复查找的次数。
- 状态转移方程:res[i - 1] = nums[i - 1] >= nums[i] ? res[i] : i;
- 通过动态规划,找到递减区间,从而可以跳过递减区间,方便快速找到大于当前值的值。后续还需要循环查找大于当前值的值。
class Solution {
public int[] nextGreaterElements(int[] nums) {
int n = nums.length;
int[] res = new int[n];
for (int i = n - 1; i > 0; i--) {
if (nums[i - 1] >= nums[i]) {
res[i - 1] = res[i];
} else {
res[i - 1] = i;
}
}
for (int i = 0; i < n; i++) {
int element = nums[i];
int j = res[i];
res[i] = -1;
do {
if (nums[j] > element) {
res[i] = nums[j];
break;
}
j++;
if (j >= n) {
j -= n;
}
} while(j != i);
}
return res;
}
}19. 第131题. 分割回文串
参考题解:回溯算法 优化
这套题的思路包括:
- 这道题应该通过深度优先搜索 + 回溯法进行求解。这样可以检查所有可能的答案,并对不可能的结果进行剪枝。
- 回文串检测部分可以通过双指针完成检测。
class Solution {
private boolean checkPalindrome(char[] charArray, int left, int right) {
while (left < right) {
if (charArray[left] != charArray[right]) {
return false;
}
left++;
right--;
}
return true;
}
private void dfs(char[] charArray, int index, int len, Deque<String> path, List<List<String>> res) {
if (index == len) {
res.add(new ArrayList<>(path));
return;
}
for (int i = index; i < len; ++i) {
if (!checkPalindrome(charArray, index, i)) {
continue;
}
path.addLast(new String(charArray, index, i + 1 - index));
dfs(charArray, i + 1, len, path, res);
path.removeLast();
}
}
public List<List<String>> partition(String s) {
int len = s.length();
List<List<String>> res = new ArrayList<>();
if (len == 0) {
return res;
}
Deque<String> stack = new ArrayDeque<>();
char[] charArray = s.toCharArray();
dfs(charArray, 0, len, stack, res);
return res;
}
}20. 第224题. 基本计算器
参考题解:java: 使用 Stack 解决
这道题的思路包括:
- 这道题要实现一个计算器,只有 + - ( ) 四种符号。
- 由于只有 + -,所以可以用 1 -1 来分别代表。
- 用栈存放字符。当为数字时,用 while 获取整个数字。当为 + - 时,用 1 -1 替代 sign。当为 ( 时,用栈存放 res 和 sign。当为 ) 时,再从栈中弹出来,用 res 进行计算。
- 这道题看着容易理解,实现起来还是有些难度的。
class Solution {
public int calculate(String s) {
Stack<Integer> stack = new Stack<Integer>();
// sign 代表正负
int sign = 1, res = 0;
int length = s.length();
for (int i = 0; i < length; i++) {
char ch = s.charAt(i);
if (Character.isDigit(ch)) {
int cur = ch - '0';
while (i + 1 < length && Character.isDigit(s.charAt(i + 1)))
cur = cur * 10 + s.charAt(++i) - '0';
res = res + sign * cur;
} else {
switch (ch) {
case '+':
sign = 1;
break;
case '-':
sign = -1;
break;
case '(':
stack.push(res);
res = 0;
stack.push(sign);
sign = 1;
break;
case ')':
res = stack.pop() * res + stack.pop();
break;
default:
}
}
}
return res;
}
}21. 第 227 题. 基本计算器 II
参考题解:基本计算器 II
这道题的思路包括:
- 由于引入了 * /,所以这道题和上一道题又不太一样。不能遇到数字就计算了,而是要遇到下一个运算符或者到结尾才能运算。
- 运算过程存放在栈中。最后再进行计算。
class Solution {
public int calculate(String s) {
Deque<Integer> stack = new LinkedList<Integer>();
char preSign = '+';
int num = 0;
int n = s.length();
for (int i = 0; i < n; ++i) {
if (Character.isDigit(s.charAt(i))) {
num = num * 10 + s.charAt(i) - '0';
}
if (!Character.isDigit(s.charAt(i)) && s.charAt(i) != ' ' || i == n - 1) {
switch (preSign) {
case '+':
stack.push(num);
break;
case '-':
stack.push(-num);
break;
case '*':
stack.push(stack.pop() * num);
break;
default:
stack.push(stack.pop() / num);
}
preSign = s.charAt(i);
num = 0;
}
}
int ans = 0;
while (!stack.isEmpty()) {
ans += stack.pop();
}
return ans;
}
}22. 第206题. 反转链表
参考题解:反转链表
这道题的思路包括:
- 反转链表是一个经典题型,最好背下来。不然现推导十分麻烦。
class Solution {
public ListNode reverseBetween(ListNode head, int left, int right) {
ListNode dummyNode = new ListNode(-1);
dummyNode.next = head;
ListNode pre = dummyNode;
for (int i = 0; i < left - 1; i++) {
pre = pre.next;
}
ListNode cur = pre.next;
ListNode next;
for (int i = 0; i < right - left; i++) {
next = cur.next;
cur.next = next.next;
next.next = pre.next;
pre.next = next;
}
return dummyNode.next;
}
}23. 第92题. 反转链表 II
参考题解:反转链表 II
这道题的思路包括:
- 同样是反转链表,同样要记下来。
- 与上一题不同的是,这个是反转中间的链表。
class Solution {
public ListNode reverseBetween(ListNode head, int left, int right) {
ListNode dummyNode = new ListNode(-1);
dummyNode.next = head;
ListNode pre = dummyNode;
for (int i = 0; i < left - 1; i++) {
pre = pre.next;
}
ListNode cur = pre.next;
ListNode next;
for (int i = 0; i < right - left; i++) {
next = cur.next;
cur.next = next.next;
next.next = pre.next;
pre.next = next;
}
return dummyNode.next;
}
}24. 第341题. 扁平化嵌套列表迭代器
24.1 DFS + 队列 实现
这道题的思路包括:
- 这道题可以用深度优先搜索处理。
- 深度优先搜索,可以用递归写,更加方便。
public class NestedIterator implements Iterator<Integer> {
Deque<Integer> queue = new ArrayDeque<>();
public NestedIterator(List<NestedInteger> nestedList) {
dfs(nestedList);
}
@Override
public Integer next() {
return hasNext() ? queue.pollFirst() : -1;
}
@Override
public boolean hasNext() {
return !queue.isEmpty();
}
void dfs(List<NestedInteger> list) {
for (NestedInteger item : list) {
if (item.isInteger()) {
queue.addLast(item.getInteger());
} else {
dfs(item.getList());
}
}
}
}24.2 递归 + 栈 实现
这道题的思路包括:
- 不对元素进行预处理,而将所有元素放入栈中,需要时再展开。
public class NestedIterator implements Iterator<Integer> {
Deque<NestedInteger> stack = new ArrayDeque<>();
public NestedIterator(List<NestedInteger> list) {
for (int i = list.size() - 1; i >= 0; i--) {
NestedInteger item = list.get(i);
stack.addLast(item);
}
}
@Override
public Integer next() {
return hasNext() ? stack.pollLast().getInteger() : -1;
}
@Override
public boolean hasNext() {
if (stack.isEmpty()) {
return false;
} else {
NestedInteger item = stack.peekLast();
if (item.isInteger()) {
return true;
} else {
item = stack.pollLast();
List<NestedInteger> list = item.getList();
for (int i = list.size() - 1; i >= 0; i--) {
stack.addLast(list.get(i));
}
return hasNext();
}
}
}
}25. 第456题. 132 模式
个人题解:单调栈求解问题
这道题的思路包括:
- 这道题应用到了一个新的数据结构:单调栈。
- 1 3 2 模式,顾名思义,就是中间比两边大,右边比左边大。
- 因此,可以首先通过一次遍历,维护一个左侧最小值列表。
- 右侧则需要维护一个单调栈,从而保存 3 和 2 对应的值。
- 单调栈,就是针对每个元素,如果栈顶比当前值小,就弹出来。进行这样一个 while 判断,直到栈为空或栈顶比当前值大为止,这时可以将当前值放进去。在弹出的过程中其实就是判断是不是 2 的过程。如果弹出元素比当前值小,比左侧最小值大,就说明这是一个 1 3 2 模式。
- 核心思路还是排序。不过,1 3 2 的左边和右边是不同规则,所以要通过一次遍历先确定左边,再通过单调栈让右侧维护递增序列。
class Solution {
public boolean find132pattern(int[] nums) {
int n = nums.length;
if (n < 3) {
return false;
}
int[] min = new int[n];
min[1] = nums[0];
for (int i = 2; i < n; ++i) {
min[i] = Math.min(min[i - 1], nums[i - 1]);
}
Deque<Integer> d = new ArrayDeque<>();
for (int i = n - 1; i > 0; --i) {
while (!d.isEmpty() && d.peek() <= nums[i]) {
int temp = d.pop();
if (temp < nums[i] && temp > min[i]) {
return true;
}
}
d.push(nums[i]);
}
return false;
}
}26. 第82题. 删除排序链表中的重复元素 II
参考题解:删除排序链表中的重复元素 II
这道题的思路包括:
- 又是链表题。一般链表题都比较烧脑,其实只要好好记忆就没事,类似动态规划。
- 因此,我在以后会将链表题、动态规划题等按照题型进行整理。这样也能更好地帮助大家。
- 遇到可能修改头结点的部分,就新建一个 dummy 作为空头结点。另一个 cur 作为当前节点。
- cur.next 用于修改指针,cur 用于调整当前节点。
class Solution {
public ListNode deleteDuplicates(ListNode head) {
if (head == null) {
return head;
}
ListNode dummy = new ListNode(0, head);
ListNode cur = head;
while (cur.next != null && cur.next.next != null) {
if (cur.next.val == cur.next.next.val) {
int x = cur.next.val;
while (cur.next != null && cur.next.val == x) {
cur.next = cur.next.next; // 调整 cur 的 next 指针。
}
} else {
cur = cur.next; // 调整 cur
}
}
return dummy.next;
}
}27. 第 90 题. 子集 II
这道题的思路包括:
- 这道题是典型的回溯法,要求目标数组的所有幂子集。
- 回溯过程,需要 set 存储子集避免重复,需要存储当前指针 index,以及当前数组 cur。后面先加入当前指向的元素,并回溯,随后再移除当前指针元素,再回溯,就可以遍历所有情况。
- 需要注意的是,如果 ans.add() 这里不是重新 new 一个数组,而是直接放 cur,结果会生成空的数组。这应该和 Collections 类型转换的内部机制有关。
class Solution {
public List<List<Integer>> subsetsWithDup(int[] nums) {
Arrays.sort(nums);
Set<List<Integer>> ans = new HashSet<>();
List<Integer> cur = new ArrayList<>();
dfs(nums, 0, cur, ans);
return new ArrayList<>(ans);
}
private void dfs(int[] nums, int index, List<Integer> cur, Set<List<Integer>> ans) {
if (nums.length == index) {
ans.add(new ArrayList<>(cur));
return;
}
cur.add(nums[index]);
dfs(nums, index + 1, cur, ans);
cur.remove(cur.size() - 1);
dfs(nums, index + 1, cur, ans);
}
}28. 第704题. 二分查找
参考题解:二分查找细节详解
这道题的思路包括:
- 二分查找一直是一个要注意的内容。我之前在纸质笔记上整理了全部内容,今天在文档上再记录一次。
- 注意!
mid = left + (right - left) >> 1这个表达式只能用在第一种方法里。后面两种用了可能会导致死循环!
28.1 基本二分查找
注意事项:
- 循环条件:left <= right
- 中间位置计算:mid = left + ((right - left) >> 1) 防止 left + right 出现溢出,移位运算提高性能
- 左边界更新:left = mid + 1
- 右边界更新:right = mid - 1
- 返回值:mid 或 -1
class BinarySearch {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] == target) {
return mid;
} else if (nums[mid] > target) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return -1;
}
}28.2 左侧边界的二分查找
注意事项:
- 循环条件:left < right
- 中间位置计算:mid = left + ((right - left) >> 1)
- 左边界更新:left = mid + 1
- 右边界更新:right = mid 要搜索左边界,搜索范围就要从右边开始,不断向左收缩
- 返回值:nums[left] == target ? left : -1
类型1:数组有序,但包含重复元素。部分有序,但不包含重复元素。
class Solution {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left < right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid;
}
}
return nums[left] == target ? left : -1;
}
}类型2:部分有序且包含重复元素。
注意事项:
- 区别只在于右边界更新更加保守。
class Solution {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
} else {
right--;
}
}
return nums[left] == target ? left : -1;
}
}28.3 右侧边界的二分查找
注意事项:
- 和左边界查找一样。
class Solution {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left < right) {
int mid = left + ((right - left) >> 1) + 1;
if (nums[mid] > target) {
right = mid - 1;
} else {
left = mid;
}
}
return nums[right] == target ? right : -1;
}
}29. 第208题. 实现 Trie 前缀树
参考题解:官方题解

这道题的思路包括:
- 前缀树就是字典树。
- 每个节点生成 26 个新树节点的数组。同时,还需要设置一个变量:是否是结束位置。
- 为啥要设置是否是结束位置呢?因为多个字共享同一个字典树分支,所以必须标明哪里是结束位置!
class Trie {
private Trie[] children;
private boolean isEnd;
public Trie() {
children = new Trie[26];
isEnd = false;
}
public void insert(String word) {
Trie node = this;
for (int i = 0; i < word.length(); i++) {
char ch = word.charAt(i);
int index = ch - 'a';
if (node.children[index] == null) {
node.children[index] = new Trie();
}
node = node.children[index];
}
node.isEnd = true;
}
public boolean search(String word) {
Trie node = searchPrefix(word);
return node != null && node.isEnd;
}
public boolean startsWith(String prefix) {
return searchPrefix(prefix) != null;
}
private Trie searchPrefix(String prefix) {
Trie node = this;
for (int i = 0; i < prefix.length(); i++) {
char ch = prefix.charAt(i);
int index = ch - 'a';
if (node.children[index] == null) {
return null;
}
node = node.children[index];
}
return node;
}
}30. 第179题. 最大数
参考题解:官方题解
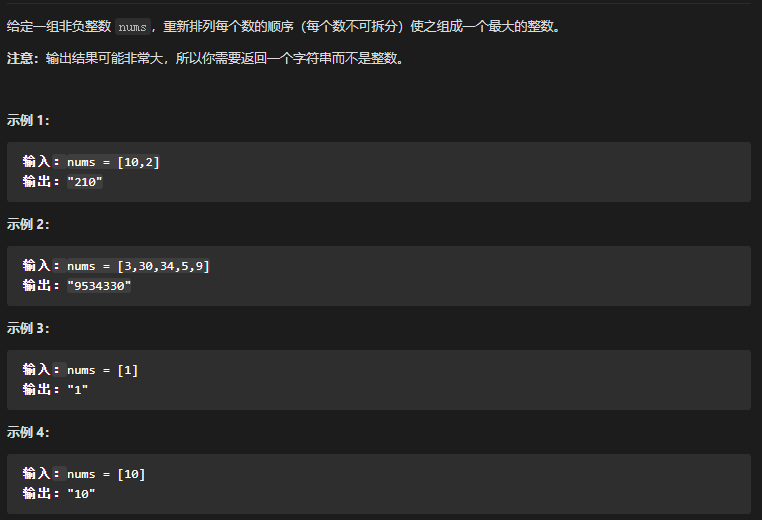
这道题的思路包括:
- 这道题最重要的就是,对有相同前缀的数字进行排序。
- 题解采用了一种非常巧妙的方式:

class Solution {
public String largestNumber(int[] nums) {
int n = nums.length;
Integer[] numsArr = new Integer[n];
for (int i = 0; i < n; i++) {
numsArr[i] = nums[i];
}
Arrays.sort(numsArr, (x, y) -> {
long sx = 10, sy = 10;
while (sx <= x) {
sx *= 10;
}
while (sy <= y) {
sy *= 10;
}
return (int) (-sy * x - y + sx * y + x);
});
if (numsArr[0] == 0) {
return "0";
}
StringBuffer ret = new StringBuffer();
for (int num : numsArr) {
ret.append(num);
}
return ret.toString();
}
}31. 第783题. 二叉搜索树节点最小距离
参考题解:官方题解
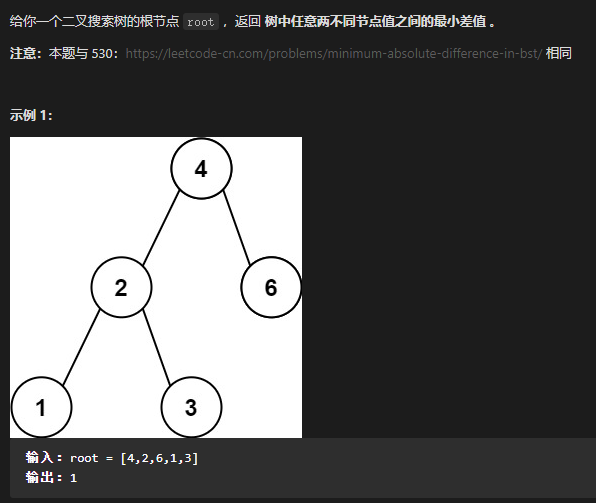
这道题的思路包括:
- 二叉搜索树的节点间最小差值,其实就是要进行一个中序遍历。
- 太久没做树的题了。其实这道题再简单不过了。
class Solution {
int min = Integer.MAX_VALUE;
TreeNode prev;
public int minDiffInBST(TreeNode root) {
inorder(root);
return min;
}
public void inorder(TreeNode root) {
if (root == null)
return;
inorder(root.left);
if (prev != null)
min = Math.min(min, root.val - prev.val);
prev = root;
inorder(root.right);
}
}32. 第220题. 存在重复元素
参考题解:官方题解
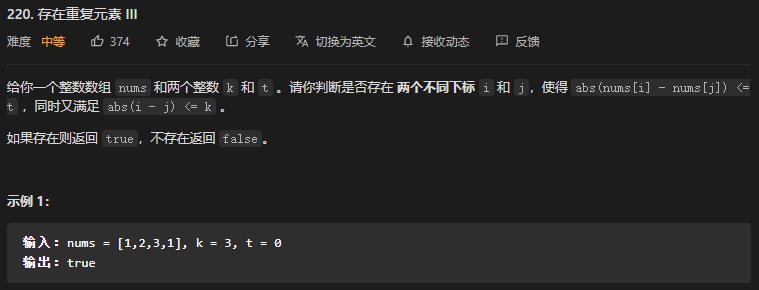
32.1 滑动窗口 + 二分查找
思路:
- 可以采用滑动窗口的方式,对于每个 i,找到有没有值在 nums[i] - t 到 nums[i] + t 内,同时滑动窗口大小必须在 i - k 和 i + k 之间。
- 二分查找,可以采用 TreeSet 数据格式。
- TreeSet.floor(),TreeSet.ceiling() 可以获取最接近 u 的上一个内容和下一个内容。如果没有,则返回 null。
class Solution {
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
int n = nums.length;
TreeSet<Long> ts = new TreeSet<>();
for (int i = 0; i < n; ++i) {
Long u = nums[i] * 1L;
Long left = ts.floor(u);
Long right = ts.ceiling(u);
if (left != null && u - left <= t) {
return true;
}
if (right != null && right - u <= t) {
return true;
}
ts.add(u);
if (i >= k) {
ts.remove(nums[i - k] * 1L);
}
}
return false;
}
}32.2 桶排序
思路:
- 另一个方法就是桶排序。设桶的大小为 t + 1,窗口大小为 k。
- 如果两个元素进了同一个桶,就说明有要求的元素。否则则是没有符合要求的。
class Solution {
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
int n = nums.length;
Map<Long, Long> map = new HashMap<Long, Long>();
long w = (long) t + 1;
for (int i = 0; i < n; i++) {
long id = getID(nums[i], w);
if (map.containsKey(id)) {
return true;
}
if (map.containsKey(id - 1) && Math.abs(nums[i] - map.get(id - 1)) < w) {
return true;
}
if (map.containsKey(id + 1) && Math.abs(nums[i] - map.get(id + 1)) < w) {
return true;
}
map.put(id, (long) nums[i]);
if (i >= k) {
map.remove(getID(nums[i - k], w));
}
}
return false;
}
public long getID(long x, long w) {
if (x >= 0) {
return x / w;
}
return (x + 1) / w - 1;
}
}33. 第28题. 实现strStr()
参考题解:简单题学 KMP 算法
思路:
- 这道题用来学习 KMP 算法,相比普通算法的 O(m * n) 复杂度,KMP 因为加入了剪枝,所以只需要 O(m + n) 复杂度。
- 朴素方法和 KMP 都是两个指针,一个指向原串,一个指向匹配串。匹配的情况下都一样往后移动。直到遇到不匹配项。朴素算法会原串指针指向下一个位置。而 KMP 算法首先会检查匹配成功的部分是否有相同
前缀和后缀,如果有,则跳转到前缀和后缀下一个位置继续匹配(原串和匹配串都会跳转)。如果匹配串对不上,则匹配串回到头部,与原串匹配。 

- 如果直接每次都检查前缀和后缀,则时间复杂度会是 O(n m m),比朴素方法还要大。因此需要利用另一个性质:匹配串的每个位置发起的匹配点,和原串无关。因此,可以用 O(m) 的算法从匹配串直接获取一个匹配点数组,也就是 next 数组。
- next 数组构建:起始时,next[0] = 0, j = 0, i = 1。循环执行,如果 p[i] == p[j],则 next[i] = j + 1, i ++, j ++;否则 循环执行:j = next[j - 1],直到 p[i] == p[j] 或 j == 0。如果 j == 0,p[i] != p[j],就 next[i] = 0, i++, j 不变。这个过程循环往复,最后给所有 next 赋值。



class Solution {
// KMP 算法
// ss: 原串(string) pp: 匹配串(pattern)
public int strStr(String ss, String pp) {
if (pp.isEmpty()) {
return 0;
}
// 分别读取原串和匹配串的长度
int n = ss.length(), m = pp.length();
// 原串和匹配串前面都加空格,使其下标从 1 开始
ss = " " + ss;
pp = " " + pp;
char[] s = ss.toCharArray();
char[] p = pp.toCharArray();
// 构建 next 数组,数组长度为匹配串的长度(next 数组是和匹配串相关的)
int[] next = new int[m + 1];
// 构造过程 i = 2,j = 0 开始,i 小于等于匹配串长度 【构造 i 从 2 开始】
for (int i = 2, j = 0; i <= m; i++) {
// 匹配不成功的话,j = next(j)
while (j > 0 && p[i] != p[j + 1]) {
j = next[j];
}
// 匹配成功的话,先让 j++
if (p[i] == p[j + 1]) {
j++;
}
// 更新 next[i],结束本次循环,i++
next[i] = j;
}
// 匹配过程,i = 1,j = 0 开始,i 小于等于原串长度 【匹配 i 从 1 开始】
for (int i = 1, j = 0; i <= n; i++) {
// 匹配不成功 j = next(j)
while (j > 0 && s[i] != p[j + 1]) {
j = next[j];
}
// 匹配成功的话,先让 j++,结束本次循环后 i++
if (s[i] == p[j + 1]) {
j++;
}
// 整一段匹配成功,直接返回下标
if (j == m) return i - m;
}
return -1;
}
}34. 第91题. 解码方法
参考题解:宫水三叶 根据数据范围切换递归和递推
思路:
-
我一开始直接使用递推解决。后来发现,这样做会指数爆炸。
-
因此,这道题是一道动态规划题。
-
dp[0] = 1; dp[i] = dp[i - 1] (if 1 <= a <= 9) dp[i] = dp[i - 1] + dp[i - 2] (if 10 <= b <= 26)
题解:
class Solution {
public int numDecodings(String s) {
int n = s.length();
s = " " + s;
char[] cs = s.toCharArray();
int[] f = new int[n + 1];
f[0] = 1;
for (int i = 1; i <= n; i++) {
int a = cs[i] - '0', b = (cs[i - 1] - '0') * 10 + (cs[i] - '0');
if (1 <= a && a <= 9) f[i] = f[i - 1];
if (10 <= b && b <= 26) f[i] += f[i - 2];
}
return f[n];
}
}35. 第53题. 最大子序和
思路:
- 动态规划,记录一下。
- 有点贪心的意思,dp 只需要一位就行,还需要一个 max。
- 因为必须有一个元素,所以 dp = nums[0] 初始化。
- 如果 dp < 0 就 dp = nums[i],重新开始,否则 dp += nums[i]。
class Solution {
public int maxSubArray(int[] nums) {
int length = nums.length;
if (length == 0) {
return 0;
}
int dp = nums[0], max = nums[0];
for (int i = 1; i < length; ++i) {
if (dp < 0) {
dp = nums[i];
} else {
dp += nums[i];
}
if (dp > max) {
max = dp;
}
}
return max;
}
}36. 第363题. 矩形区域不超过 K 的最大数值和
参考题解:Java 从暴力开始优化,配图配注释
问题:
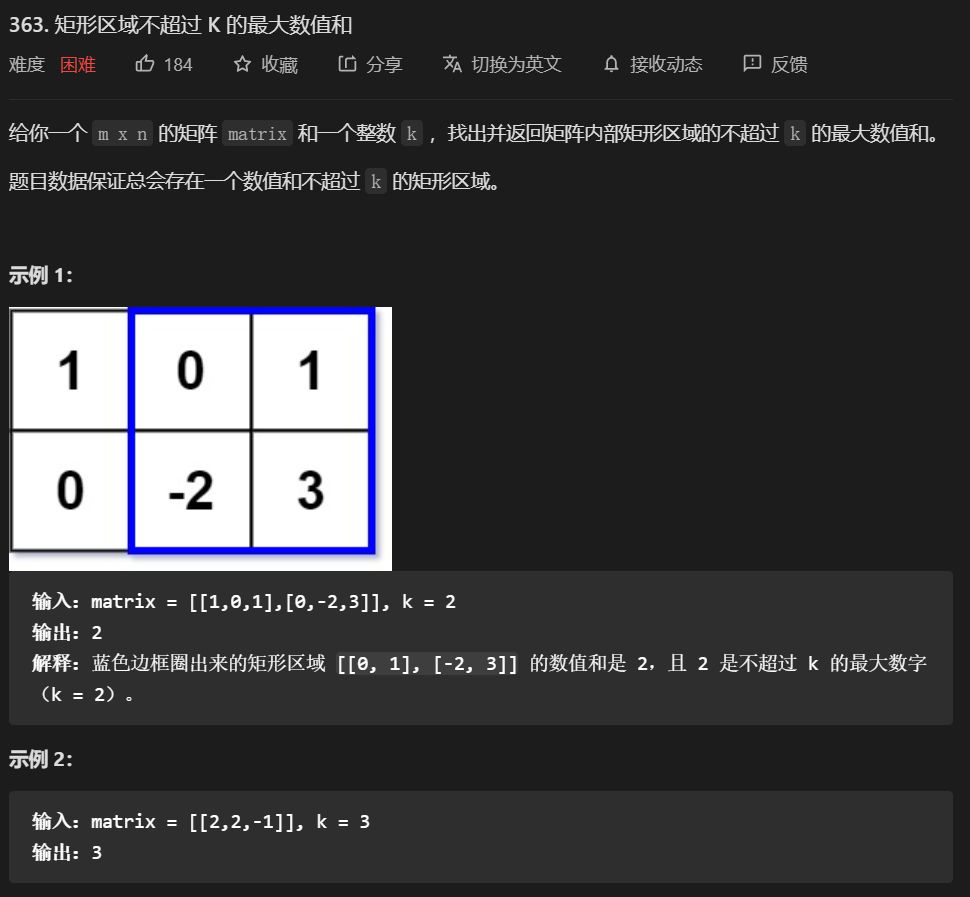
思路:
- 这道题相当不错,涉及到两个思路。
- 首先,将二维转化为一维问题。也就是,上下边界不动,左右边界遍历移动,同时计算中间每一行的总和。这样就能方便的将问题转化为1维最大子序列和的问题。
- 同时,由于设置了不能超过 k,因此还不能简单将问题就理解为子序列和。当最大子序列和求得的答案超过 k 时,就只能用暴力法求解。
- 思想很好理解,实现很容易出现问题。要注意里面每一步是如何实现的。
题解:
class Solution {
public int maxSumSubmatrix(int[][] matrix, int k) {
int r = matrix.length, c = matrix[0].length, res = 0;
int max = Integer.MIN_VALUE;
for (int i = 0; i < c; ++i) {
int[] sum = new int[r];
for (int j = i; j < c; ++j) {
for (int h = 0; h < r; ++h) {
sum[h] += matrix[h][j];
}
max = Math.max(max, getMax(sum, k));
if (max == k) {
return k;
}
}
}
return max;
}
public int getMax(int[] sum, int k) {
int dp = sum[0], max = sum[0], length = sum.length;
for (int i = 1; i < length; ++i) {
if (dp <= 0) {
dp = sum[i];
} else {
dp += sum[i];
}
if (dp > max) {
max = dp;
}
}
if (max <= k) {
return max;
}
max = Integer.MIN_VALUE;
for (int i = 0; i < length; ++i) {
int s = 0;
for (int j = i; j < length; ++j) {
s += sum[j];
if (s > max && s <= k) {
max = s;
}
if (max == k) {
return k;
}
}
}
return max;
}
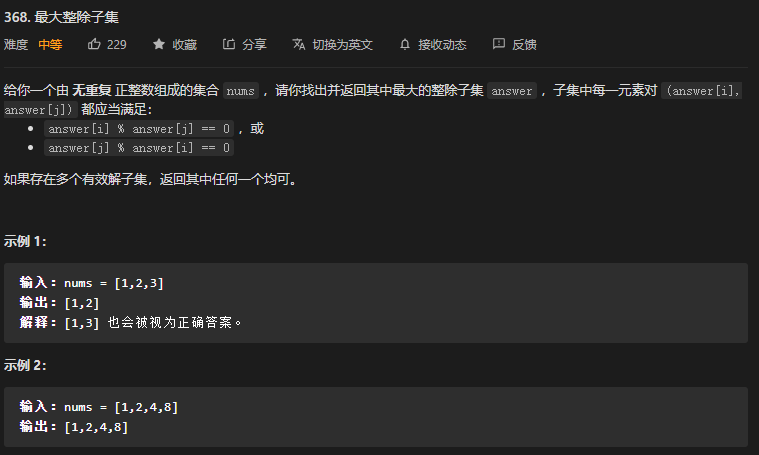
}37. 第368题. 最大整除子集
参考:官方题解
问题:
思路:
- 这道题采用动态规划。是一道之前没有总结过的动态规划题。
- 首先排序,随后 dp 记录包含第 i 个元素的最大整除数组大小。
dp[i] = Math.max(dp[i], dp[j] + 1);。 - 最后,从后往前重新构建最大整除数组。需要迭代
maxVal和maxNum。
题解:
class Solution {
public List<Integer> largestDivisibleSubset(int[] nums) {
int len = nums.length;
Arrays.sort(nums);
// 第 1 步:动态规划找出最大子集的个数、最大子集中的最大整数
int[] dp = new int[len];
Arrays.fill(dp, 1);
int maxSize = 1;
int maxVal = nums[0];
for (int i = 1; i < len; i++) {
for (int j = 0; j < i; j++) {
// 题目中说「没有重复元素」很重要
if (nums[i] % nums[j] == 0) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
if (dp[i] > maxSize) {
maxSize = dp[i];
maxVal = nums[i];
}
}
// 第 2 步:倒推获得最大子集
List<Integer> res = new ArrayList<Integer>();
if (maxSize == 1) {
res.add(nums[0]);
return res;
}
for (int i = len - 1; i >= 0 && maxSize > 0; i--) {
if (dp[i] == maxSize && maxVal % nums[i] == 0) {
res.add(nums[i]);
maxVal = nums[i];
maxSize--;
}
}
return res;
}
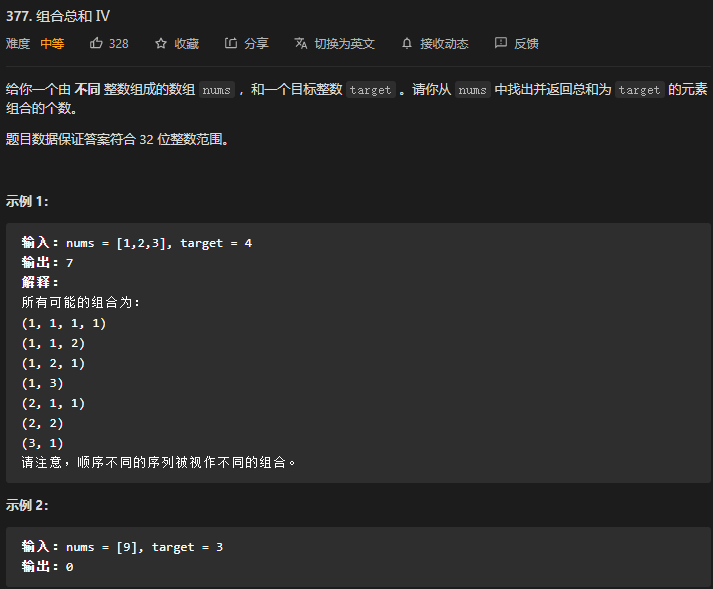
}38. 第377题. 组合总和 4
参考题解:官方题解
问题:
思路:
- 这道题一看就发现,和爬梯子是一样的。
- 难点在于:爬梯子一般只有两个步伐,一次一层和一次两层,而这个有 nums 种步伐。
- 其实办法就是:在内部加一个遍历,如果步伐比梯子数少,就加上那个减去那个步伐的 dp 的状态。这样其实就和爬梯子一样了。
题解:
class Solution {
public int combinationSum4(int[] nums, int target) {
int length = nums.length;
int[] dp = new int[target + 1];
dp[0] = 1;
for (int i = 1; i <= target; ++i) {
for (int j = 0; j < length; ++j) {
if (nums[j] <= i) {
dp[i] += dp[i - nums[j]];
}
}
}
return dp[target];
}
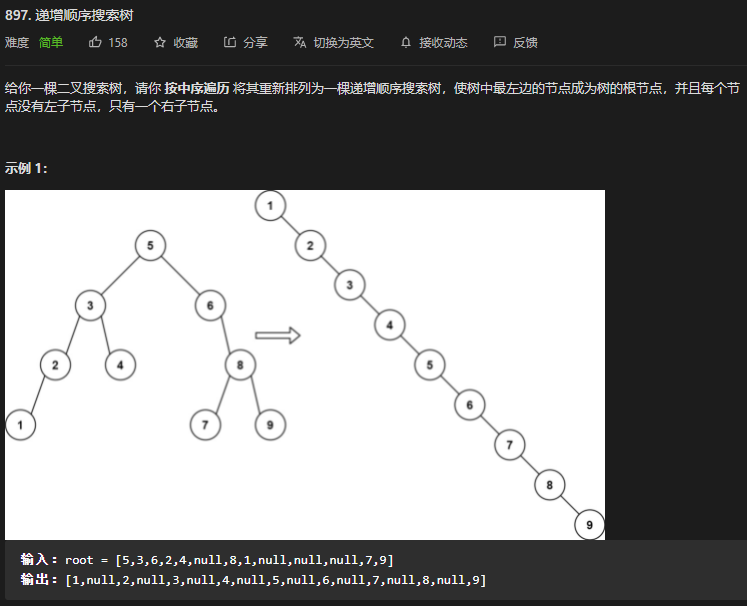
}39. 第897题. 递增顺序搜索树
参考题解:官方题解
问题:
思路:
- 这道题就是中序遍历。这里感觉要注意几点,能更加专业:
- 哨兵节点命名为 dummy,当前节点命名为 cur。前序遍历命名为 preorder,中序遍历命名为 inorder,后序遍历命名为 postorder。
题解:
class Solution {
public TreeNode increasingBST(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
inorder(root, res);
TreeNode dummyNode = new TreeNode(-1);
TreeNode curNode = dummyNode;
for (int val : res) {
curNode.right = new TreeNode(val);
curNode = curNode.right;
}
return dummyNode.right;
}
public void inorder(TreeNode root, List<Integer> res) {
if (root != null) {
inorder(root.left, res);
res.add(root.val);
inorder(root.right, res);
}
}
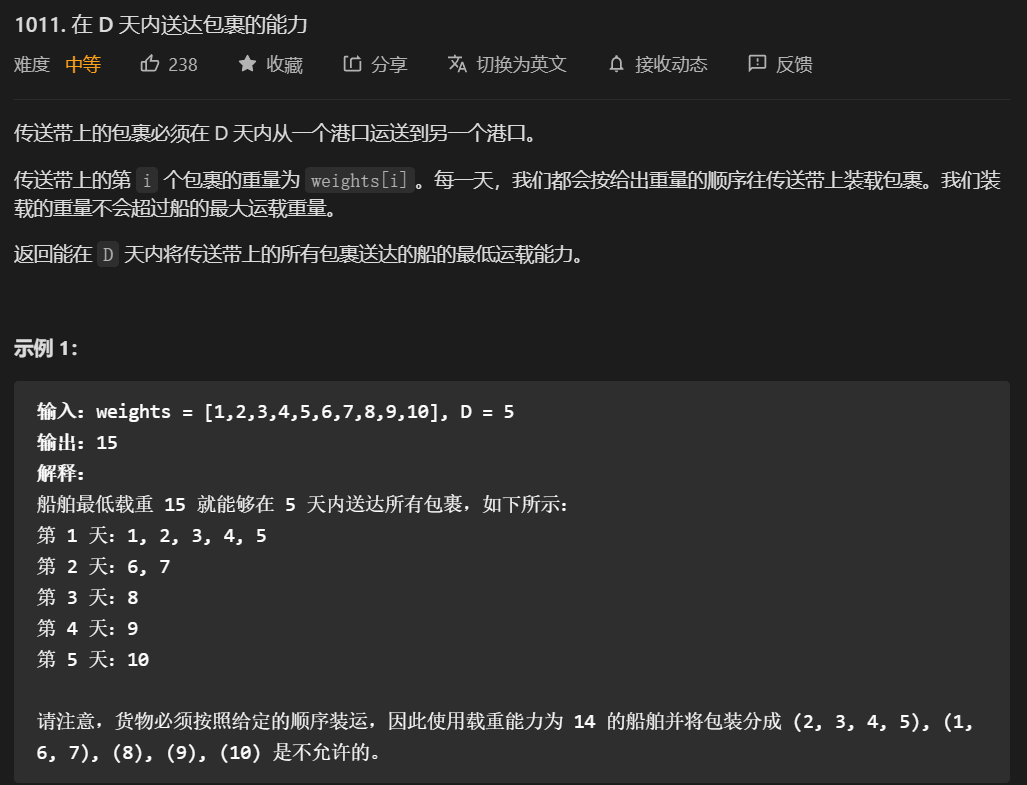
}40. 第1011题. 在 D 天内送达包裹的能力
参考题解:官方题解
问题:
思路:
- 这道题我一开始以为是动态规划,毕竟满足了最值问题和条件转移的思路。一看题解,看来道行还是不够,这是二分查找。
- 这道题是一道带判断的二分查找。
- 左边界是最大货物重量,右边界是总体重量。
题解:
class Solution {
public int shipWithinDays(int[] weights, int D) {
// 确定二分查找左右边界
int left = Arrays.stream(weights).max().getAsInt(), right = Arrays.stream(weights).sum();
while (left < right) {
int mid = (left + right) / 2;
// need 为需要运送的天数
// cur 为当前这一天已经运送的包裹重量之和
int need = 1, cur = 0;
for (int weight : weights) {
if (cur + weight > mid) {
++need;
cur = 0;
}
cur += weight;
}
if (need <= D) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
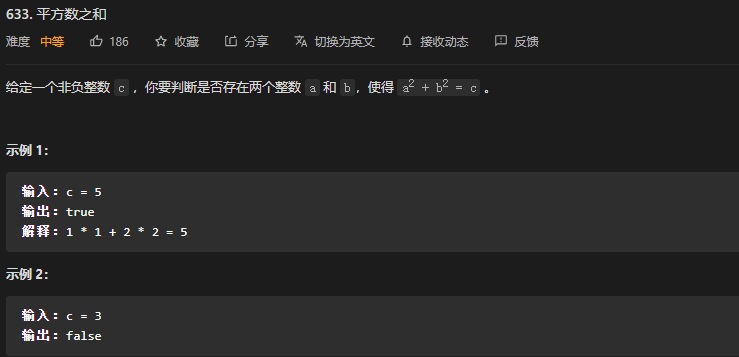
}41. 第633题. 平方数之和
参考题解:官方题解
题目:
思路:
- 这道题其实蛮简单的,我用 TreeSet 配合 0 到 sqrt 扫描过了。
- 但是答案提供了另一种思路:双指针。
- 左指针为 0, 右指针为 sqrt(c),然后往中间找就行。
题解:
class Solution {
public boolean judgeSquareSum(int c) {
int left = 0;
int right = (int) Math.sqrt(c);
while (left <= right) {
int sum = left * left + right * right;
if (sum == c) {
return true;
} else if (sum > c) {
right--;
} else {
left++;
}
}
return false;
}
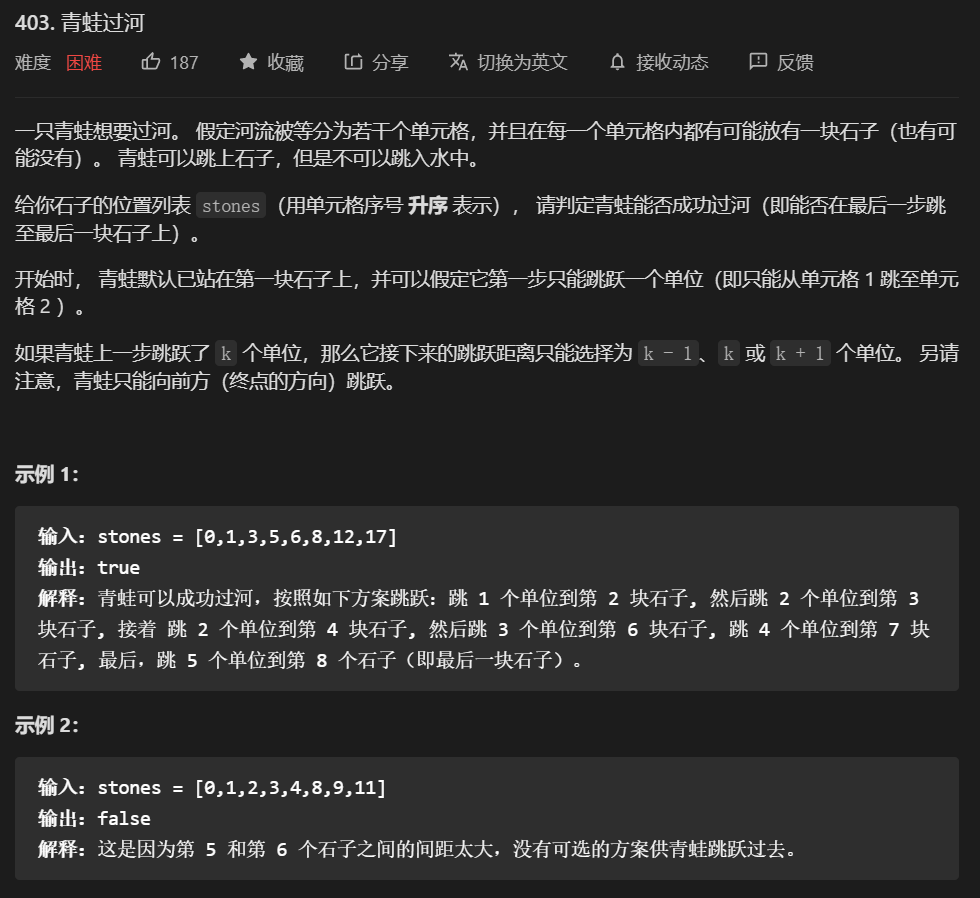
}42. 第403题. 青蛙过河
参考题解:官方题解
问题:
标签:
- 动态规划。
思路:
- 这是一道典型的动态规划题。
- 用二维布尔数组存储状态。
DP[0][0]为初始状态为 true。 - 状态转移
DP[I][K] = DP[J][K - 1] || DP[J][K] || DP[J][K + 1]。 - 当两个石头间距大于 i 时没有答案。
题解:
class Solution {
public boolean canCross(int[] stones) {
int n = stones.length;
boolean[][] dp = new boolean[n][n];
dp[0][0] = true;
for (int i = 1; i < n; ++i) {
if (stones[i] - stones[i - 1] > i) {
return false;
}
}
for (int i = 1; i < n; ++i) {
for (int j = i - 1; j >= 0; --j) {
int k = stones[i] - stones[j];
if (k > j + 1) {
break;
}
dp[i][k] = dp[j][k - 1] || dp[j][k] || dp[j][k + 1];
if (i == n - 1 && dp[i][k]) {
return true;
}
}
}
return false;
}
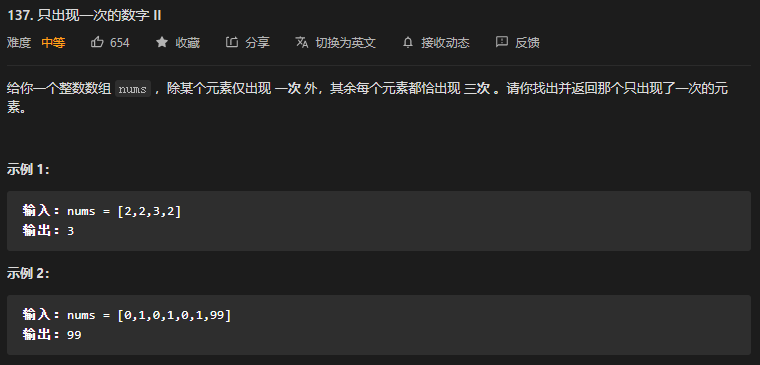
}43. 第137题. 只出现一次的数字2
参考题解:官方题解
问题:
标签:
- 位运算。
思路:
- 对每一位都求和,然后 % 3。如果不为 0,结果就与它
|=一下。 - 难点1:
sum += ((num >> i) & 1); - 难点2:
if (sum % 3 == 1) {res |= (1 << i)}; - 上面两个写的都非常漂亮巧妙。
题解:
class Solution {
public:
int singleNumber(vector<int>& nums) {
int res = 0;
for (int i = 0; i < 32; i++) {
int sum = 0;
for (int num : nums) {
sum += ((num >> i) & 1);
}
if (sum % 3 == 1) {
res |= (1 << i);
}
}
return res;
}
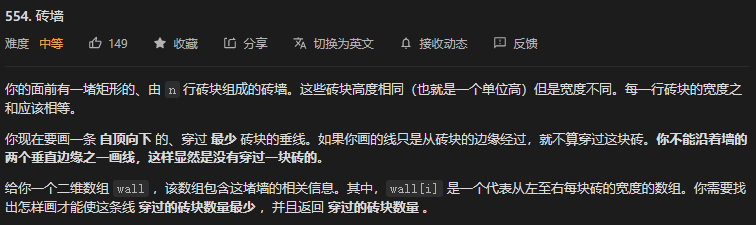
};44. 第554题. 砖墙
参考题解:官方题解
问题:
标签:
- 哈希表。
- 意想不到的方法。
思路:
- 这道题,我本以为是动态规划之类的,没想到是哈希表。
- 由于穿过的砖块加上边缘的总和是定值,因此目标是让穿过的边缘最多,这样砖块就最少了。
- 然后用哈希表进行统计即可。
题解:
class Solution {
public int leastBricks(List<List<Integer>> wall) {
Map<Integer, Integer> cnt = new HashMap<Integer, Integer>();
for (List<Integer> widths : wall) {
int n = widths.size();
int sum = 0;
for (int i = 0; i < n - 1; i++) {
sum += widths.get(i);
cnt.put(sum, cnt.getOrDefault(sum, 0) + 1);
}
}
int maxCnt = 0;
for (Map.Entry<Integer, Integer> entry : cnt.entrySet()) {
maxCnt = Math.max(maxCnt, entry.getValue());
}
return wall.size() - maxCnt;
}
}45. 第7题. 整数反转
参考题解:官方题解
题目:
标签:
- 意想不到。
思路:
- 这道题难点在于,环境不允许存储超过32位的整数,包括符号位。
- 其实符号位可以理解为一定会占用一位。最大数和最小数可以用 Integer.MAX_VALUE 和 Integer.MIN_VALUE。这样就清晰、简单了。
题解:
class Solution {
public int reverse(int x) {
int rev = 0;
while (x != 0) {
if (rev < Integer.MIN_VALUE / 10 || rev > Integer.MAX_VALUE / 10) {
return 0;
}
int digit = x % 10;
x /= 10;
rev = rev * 10 + digit;
}
return rev;
}
}46. 第1482题. 制作 m 束花所需的最少天数
参考题解:小明种花(推荐!清晰易懂又可爱的题解)
题目:
标签:
- 二分查找。
思路:
- 这道题和前面介绍的 40 题,也就是 1011 题码头运货特别像。
- 二分查找,边界是天数。然后根据 mid 指向的天数,找到符合要求又天数最少的答案。
题解:
class Solution {
public int minDays(int[] bloomDay, int m, int k) {
int n = bloomDay.length;
if (m * k > n) {
return -1;
}
int left = Arrays.stream(bloomDay).min().getAsInt(), right = Arrays.stream(bloomDay).max().getAsInt();
while (left < right) {
int mid = (left + right) >> 1;
int numMake = 0, numBloom = 0;
for (int i : bloomDay) {
if (i <= mid) {
numBloom ++;
} else {
numBloom = 0;
}
if (numBloom == k) {
numMake ++;
numBloom = 0;
}
}
if (numMake >= m) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
}47. 1310题. 子数组异或查询
个人题解:前缀和求异或
题目:
标签:
- 位操作。
思路:
- 这道题难就难在,边界条件。
- 一开始边界条件判断错,很有可能会慌乱。这在面试中也很容易造成问题。
- 边界条件就是,需要在最前面添加一个0,来避免 left 为 0 的情况。右边界是闭的,所以右边界要 + 1。认清这一点就好办了。
题解:
class Solution {
public int[] xorQueries(int[] arr, int[][] queries) {
int length = arr.length;
int[] dp = new int[length + 1];
dp[0] = 0;
for (int i = 1; i <= length; ++i) {
dp[i] = dp[i - 1] ^ arr[i - 1];
}
int length_q = queries.length;
int[] res = new int[length_q];
for (int i = 0; i < length_q; ++i) {
int left = queries[i][0], right = queries[i][1] + 1;
res[i] = dp[right] ^ dp[left];
}
return res;
}
}48. 第12、13题. 罗马数字与整数的转换
参考题解:
题目:
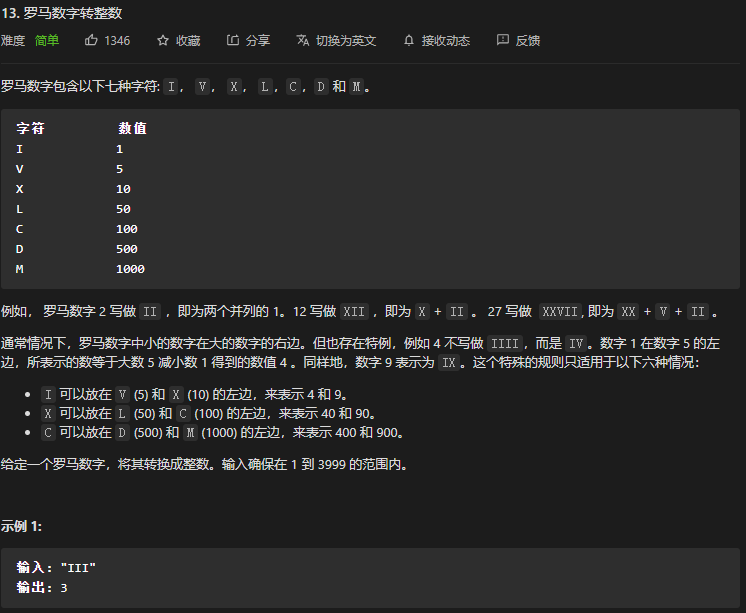
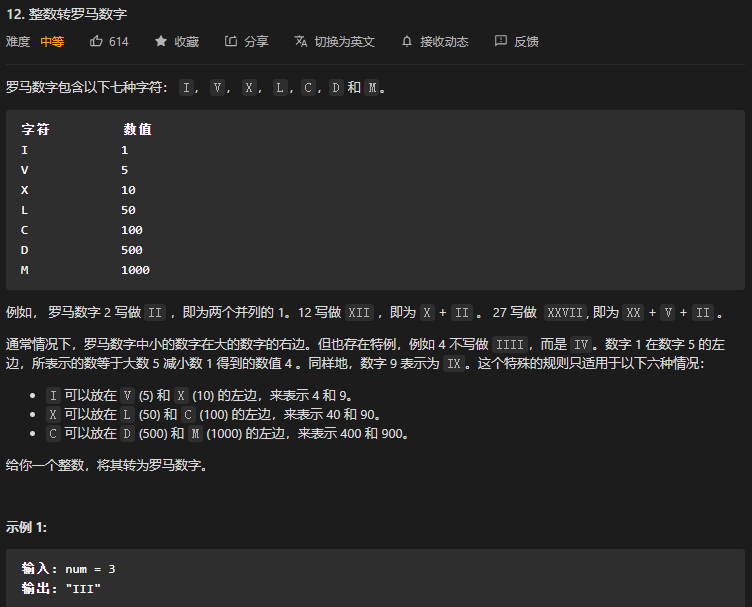
标签:
- 贪心法。
思路:
- 两道题都是贪心法,这是不容易想到的,需要背下来。
- 第一道题从大到小构建数组即可。第二道题需要构建字典。都非常考验编程能力。
题解:
public class Solution {
public String intToRoman(int num) {
int[] nums = {1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};
String[] romans = {"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"};
StringBuilder stringBuilder = new StringBuilder();
int index = 0;
while (index < 13) {
while (num >= nums[index]) {
stringBuilder.append(romans[index]);
num -= nums[index];
}
index++;
}
return stringBuilder.toString();
}
}class Solution {
Map<Character, Integer> map = new HashMap<>() {{
put('I', 1);
put('V', 5);
put('X', 10);
put('L', 50);
put('C', 100);
put('D', 500);
put('M', 1000);
}};
public int romanToInt(String s) {
int res = 0, n = s.length();
for (int i = 0; i < n; ++i) {
int value = map.get(s.charAt(i));
if (i != n - 1 && map.get(s.charAt(i + 1)) > value) {
res -= value;
} else {
res += value;
}
}
return res;
}
}49. 692题. 前 K 个高频单词
参考题解:官方题解
题目:
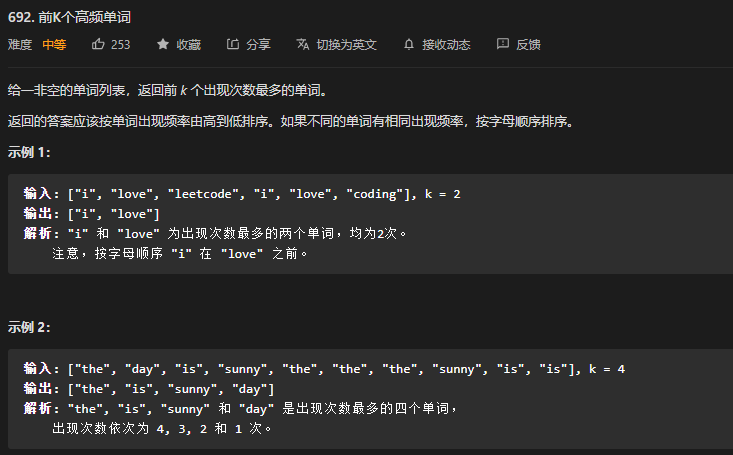
标签:
- 哈希表。
- 排序。
思路:
- 这道题很考验编码能力。涉及到了:哈希表、排序改写。
- 难点1:
map.put(word, map.getOrDefault(word, 0) + 1); - 难点2:
for (Map.Entry<String, Integer> entry : map.entrySet()) - 难点3:
Collections.sort(res, new Comparator<String>()) {@Override public int compare(String s1, String s2)} - 难点4:
return map.get(s1) == map.get(s2) ? s1.compareTo(s2) : map.get(s2) - map.get(s1)。注意顺序 - 考虑 res 和 map 进行结合也是一个难点。
题解:
class Solution {
public List<String> topKFrequent(String[] words, int k) {
HashMap<String, Integer> map = new HashMap<>();
for (String word : words) {
map.put(word, map.getOrDefault(word, 0) + 1);
}
List<String> res = new ArrayList<>();
for (Map.Entry<String, Integer> entry : map.entrySet()) {
res.add(entry.getKey());
}
Collections.sort(res, new Comparator<String>() {
@Override
public int compare(String s1, String s2) {
return map.get(s1) == map.get(s2) ? s1.compareTo(s2) : map.get(s2) - map.get(s1);
}
});
return res.subList(0, k);
}
}50. 第664题. 奇怪的打印机
参考题解:官方题解
题目:
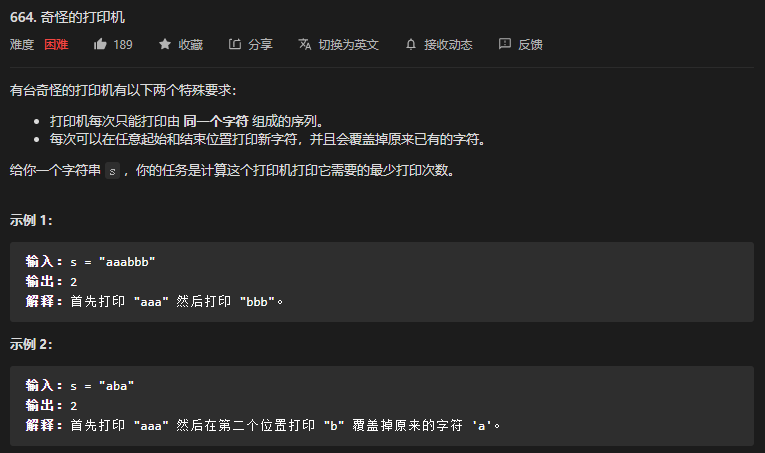
标签:
- 动态规划。
思路:
-
可以转化为 i 到 j 之间的打印最少次数。
-
初始条件:
dp[i][i] = 1。 -
转移条件:如果字符串在 i 的位置和 j 的位置一样,则可以考虑前一个点,也就是
dp[i][j] = dp[i][j - 1]。否则,考虑中间一个 k ,前半部分和后半部分求和,取最小值。 -
为了确保动态规划计算顺序,需要左指针 i 从右往左,右指针 j 从左往右。当然右指针必须在左指针右边。
题解:
class Solution {
public int strangePrinter(String s) {
int length = s.length();
int[][] dp = new int[length][length];
for (int i = 0; i < length; ++i) {
dp[i][i] = 1;
}
for (int i = length - 1; i >= 0; --i) {
for (int j = i + 1; j < length; ++j) {
if (s.charAt(i) == s.charAt(j)) {
dp[i][j] = dp[i][j - 1];
} else {
int m = Integer.MAX_VALUE;
for (int k = i; k < j; ++k) {
int temp = dp[i][k] + dp[k + 1][j];
if (temp < m) {
m = temp;
}
}
dp[i][j] = m;
}
}
}
return dp[0][length - 1];
}
}51. 第1990题. 反转每队括号间的子串
参考题解:官方题解
题目:
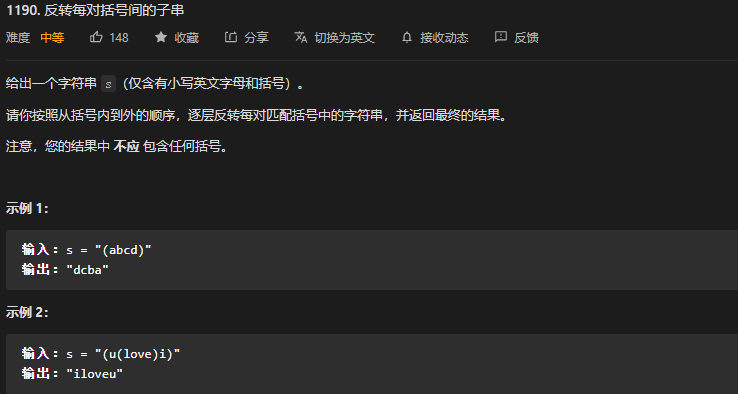
标签:
- 栈。
思路:
- 这道题一看就是栈。这种括号类型的都是栈。
- 不过,实现起来还是有一点难度的。这里就用了 StringBuffer,必须要熟悉相应的操作。
- StringBuffer 操作:setLength, reverse, insert, append, toString。
题解:
class Solution {
public String reverseParentheses(String s) {
Deque<String> stack = new LinkedList<>();
StringBuffer sb = new StringBuffer();
for (int i = 0; i < s.length(); ++i) {
char ch = s.charAt(i);
if (ch == '(') {
stack.push(sb.toString());
sb.setLength(0);
} else if (ch == ')') {
sb.reverse();
sb.insert(0, stack.pop());
} else {
sb.append(ch);
}
}
return sb.toString();
}
}52. 第461题. 汉明距离
参考题解:官方题解
题目:
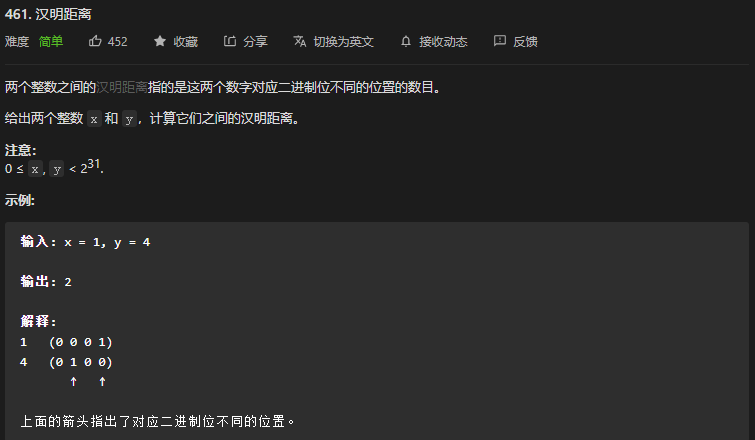
标签:
- 位运算。
思路:
- 这道题包括了位运算的典型内容。
- 比较不同位置,首先要求异或,然后针对每一位,要用与运算,获取每一位是否为1。最后,通过位移运算移动数。
题解:
class Solution {
public int hammingDistance(int x, int y) {
int res = 0, val = x ^ y;
while (val != 0) {
res += val & 1;
val >>= 1;
}
return res;
}
}53. 第477题. 汉明距离总和
参考题解:官方题解
题目:
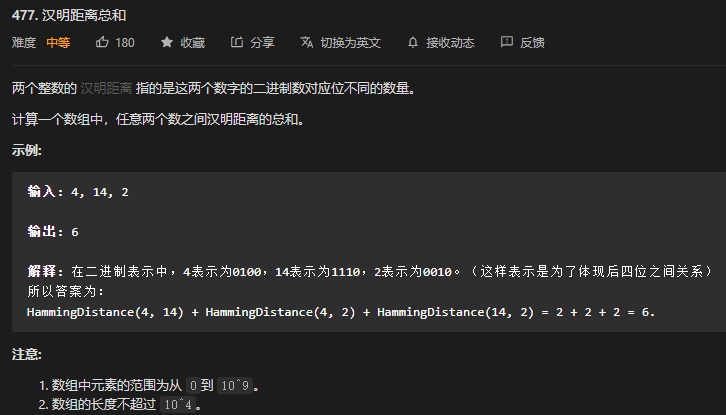
标签:
- 位运算。
- 意想不到。
- 数学。
思路:
- 这道题和前面的一道题,汉明距离,是比较相关的。但是,那道题的方法如果直接拿过来用,会超时的。暴力法。但是需要使用 Integer.bitCount() 方法,才能暴力法,不然时间和空间都会超。
- 数学方法:针对32位的 Int 的每一位统计 1 的个数。两两之间的不同位置之和为 c * (n - c),其中 c 是 1 的个数,n - c 是 0 的个数。
题解:
-
第一种题解:暴力法。
-
class Solution { public int totalHammingDistance(int[] nums) { ArrayListarrayListA = new ArrayList<>(); int length = nums.length, res = 0; for (int i = 0; i < length - 1; ++i) { for (int j = i + 1; j < length; ++j) { res += Integer.bitCount(nums[i] ^ nums[j]); } } return res; } } -
第二种题解:数学方法。
-
class Solution { public int totalHammingDistance(int[] nums) { int ans = 0, n = nums.length; for (int i = 0; i < 30; ++i) { int c = 0; for (int val : nums) { c += (val >> i) & 1; } ans += c * (n - c); } return ans; } }
54. 第560题. 和为 K 的子数组
参考题解:官方题解
题目:
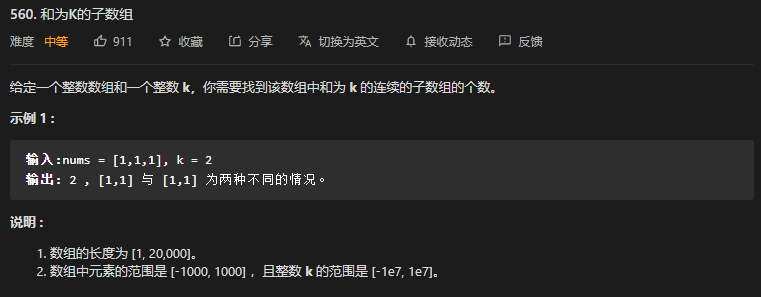
标签:
- 哈希表。
- 前缀和。
- 意想不到。
思路:
- 这道题常规思路就是 O(n ^ 2) 的遍历。
- 然而,还有一种简单方法:哈希表。
- 查找指定 Key: map.containsKey()。
题解:
public class Solution {
public int subarraySum(int[] nums, int k) {
int count = 0, pre = 0;
HashMap<Integer, Integer> map = new HashMap<>();
map.put(0, 1);
for (int i = 0; i < nums.length(); ++i) {
pre += nums[i];
if (map.containsKey(pre - k)) {
count += map.get(pre - k);
}
map.put(pre, map.getOrDefault(pre, 0) + 1);
}
return count;
}
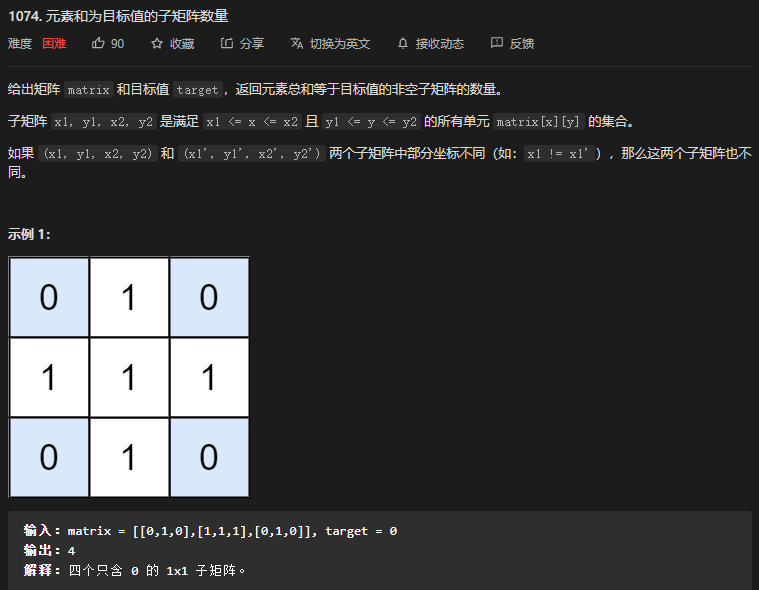
}55. 第1074题. 元素和为目标值的子矩阵数量
参考题解:官方题解
题目:
标签:
- 哈希表。
- 前缀和。
- 意想不到。
思路:
-
同样是前缀和加哈希表。不过需要根据矩形做一个变换。需要固定上边界,遍历下边界和列。
-
for (int i = 0; i < m; ++i) { for (int j = i; j < m; ++j) { for (int k = 0; k < n; ++k) { ... } } }
题解:
class Solution {
public int numSubmatrixSumTarget(int[][] matrix, int target) {
int ans = 0;
int m = matrix.length, n = matrix[0].length;
for (int i = 0; i < m; ++i) { // 枚举上边界
int[] sum = new int[n];
for (int j = i; j < m; ++j) { // 枚举下边界
for (int c = 0; c < n; ++c) {
sum[c] += matrix[j][c]; // 更新每列的元素和
}
ans += subarraySum(sum, target);
}
}
return ans;
}
public int subarraySum(int[] nums, int k) {
Map<Integer, Integer> map = new HashMap<Integer, Integer>();
map.put(0, 1);
int count = 0, pre = 0;
for (int x : nums) {
pre += x;
if (map.containsKey(pre - k)) {
count += map.get(pre - k);
}
map.put(pre, map.getOrDefault(pre, 0) + 1);
}
return count;
}
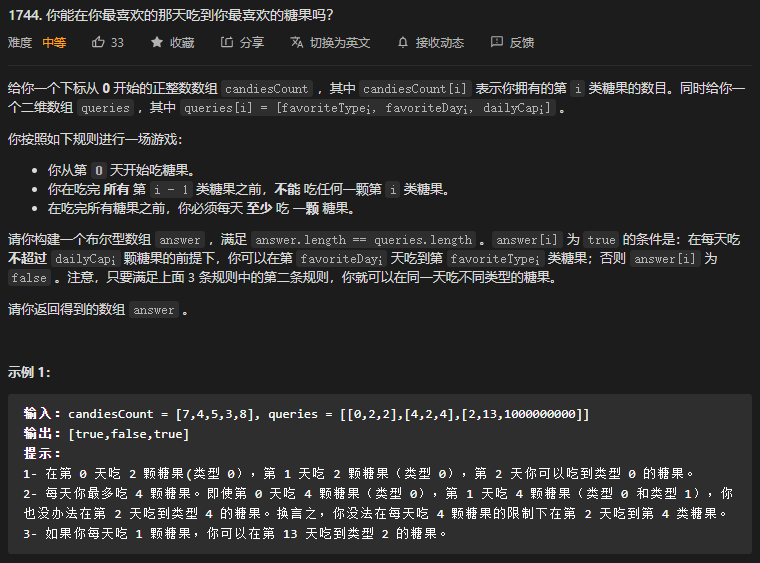
}56. 第1744题. 你能在你最喜欢的那天吃到你最喜欢的糖果吗?
个人题解:前缀和求解问题
题目:
标签:
- 恶心。
思路:
- 这道题是考察前缀和。这个没什么难的。难点在于,如何通过所有样例!
- 难点1:采用 long 保存元素,避免溢出问题!
- 难点2:long fu = (long)(favoriteDay + 1) * dailyCap; 这里面如果不加一个强制转换,会导致结果溢出!原因是里面乘法元素全部都是 int 形的,直接乘会导致按照 int 形计算,最后返回一个 int 形给 long,不会报错,但结果不正确!!
题解:
class Solution {
public boolean[] canEat(int[] candiesCount, int[][] queries) {
int length = queries.length, candy_length = candiesCount.length;
long[] pre_candy = new long[candy_length];
pre_candy[0] = candiesCount[0];
for (int i = 1; i < candy_length; ++i) {
pre_candy[i] = pre_candy[i - 1] + candiesCount[i];
}
boolean[] res = new boolean[length];
for (int i = 0; i < length; ++i) {
int favoriteType = queries[i][0], favoriteDay = queries[i][1], dailyCap = queries[i][2];
long fl = favoriteDay + 1;
long fu = (long)(favoriteDay + 1) * dailyCap;
long dl = 1;
long du = pre_candy[favoriteType];
if (favoriteType > 0) {
dl = pre_candy[favoriteType - 1] + 1;
}
if (fl > du || fu < dl) {
res[i] = false;
} else {
res[i] = true;
}
}
return res;
}
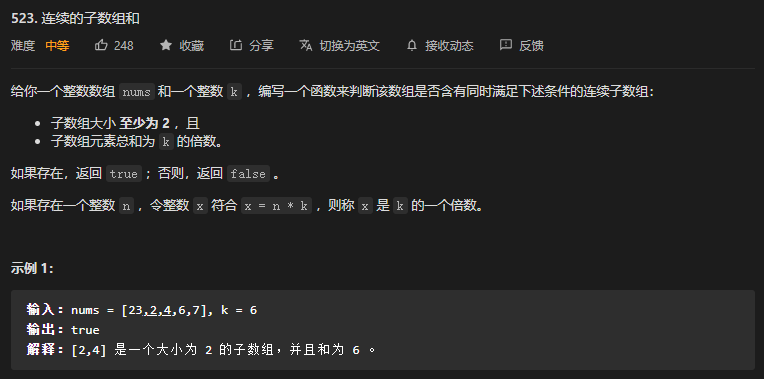
}57. 第523题. 连续的子数组和
参考题解:官方题解
题目:
标签:
- 意想不到。
- 数学。
- 恶心。
思路:
- 这道题其实是考验数学的。
- 很多题都是这样,前缀和要和哈希表配合。
- 以后看到前缀和,第一时间就要考虑到是不是和哈希表要配合。
- 和哈希表配合,就要找到规律。
- 这道题的规律就是,连续数组值要是 k 的倍数,那前后端的前缀和相对于 k 的余数就要相等。因此,只需要一遍扫描就可以,当扫描到后端的余数时,就要检查是否有前端的余数和它相等。如果相等,并且数组大小符合要求,就可以返回 true 了。
题解:
class Solution {
public boolean checkSubarraySum(int[] nums, int k) {
int length = nums.length;
if (length < 2) {
return false;
}
HashMap<Integer, Integer> map = new HashMap<>();
int[] prefix = new int[length + 1];
map.put(0, 0);
for (int i = 1; i <= length; ++i) {
prefix[i] = prefix[i - 1] + nums[i - 1];
int remain = prefix[i] % k;
if (map.containsKey(remain)) {
int index = map.get(remain);
if (i - index >= 2) {
return true;
}
} else {
map.put(remain, i);
}
}
return false;
}
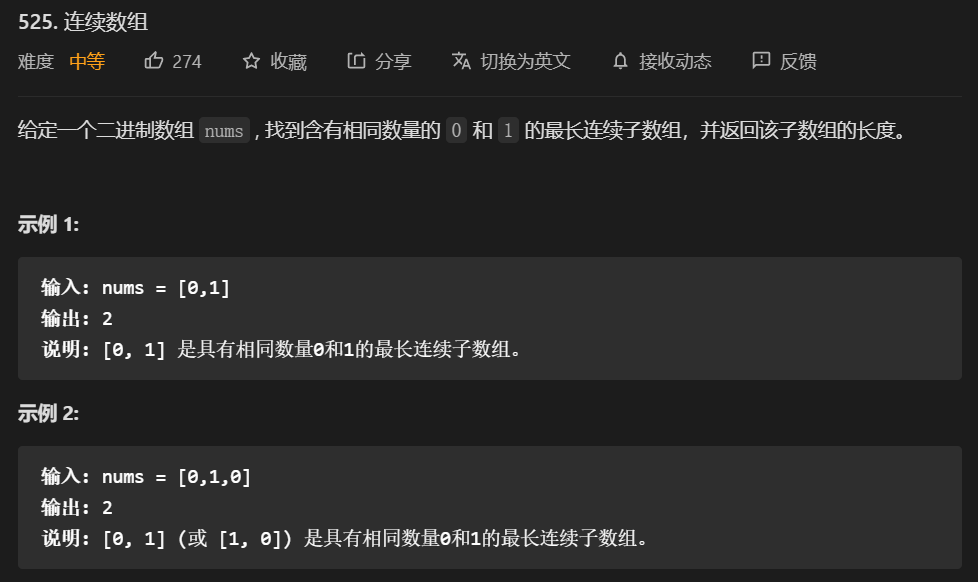
}58. 第525题. 连续数组
个人题解:前缀和哈希表求解问题
题目:
标签:
- 前缀和
- 哈希表
思路:
- 最近这些天的每日一题都是前缀和配哈希表,仔细一看,共通之处确实比较多。
- 我们把 0 转换为 -1,就变成了求最长子数组的和为 0。
- 这里要注意,更新哈希表的位置要放在最后,不然就会覆盖掉查询。
- 同时,如果前面有哈希表对应的 key 了,就不要再更新了。这样可以保留最靠前的位置,算是一个贪心策略。
题解:
class Solution {
public int findMaxLength(int[] nums) {
int length = nums.length, max = 0;
int[] prefix = new int[length + 1];
HashMap<Integer, Integer> map = new HashMap<>();
map.put(0, 0);
for (int i = 1; i <= length; ++i) {
int temp1 = nums[i - 1] == 0 ? -1 : 1;
prefix[i] = prefix[i - 1] + temp1;
if (map.containsKey(prefix[i])) {
int temp2 = i - map.get(prefix[i]);
if (max < temp2) {
max = temp2;
}
continue;
}
map.put(prefix[i], i);
}
return max;
}
}59. 第1239题. 串联字符串的最大长度
参考题解:[官方题解]()
题目:
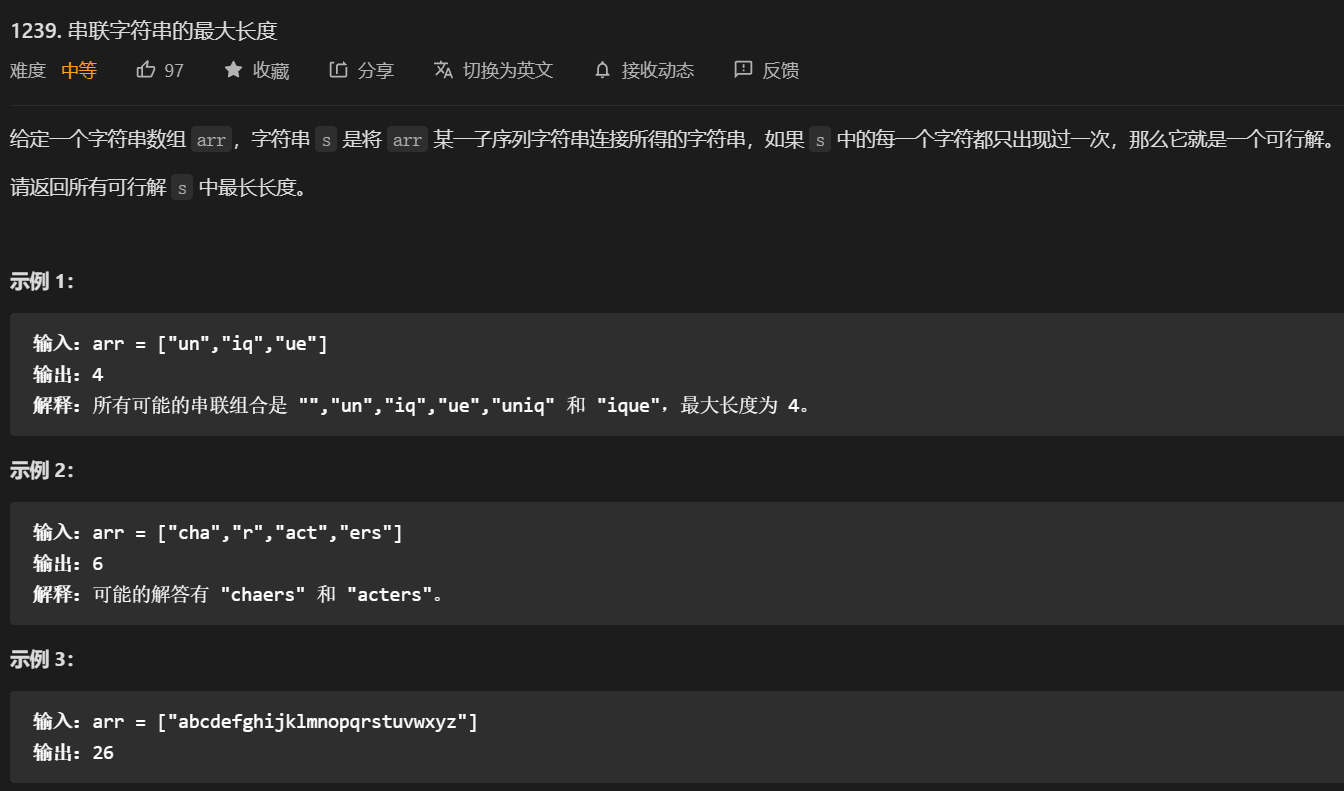
标签:
- 回溯法。
- 位运算。
思路:
- 这道题我一开始以为是双指针。但后面才发现,这道题是子序列!!
- 子串和子序列的区别:子串是连续的,子序列可以是不连续的。
- 因此,子序列这种问题就应该用回溯法来求解。
- 首先构建一个基础数组 masks,检查每个数组元素是否可以作为一个基础值,如果可以,则将值添加到 masks 中,如果不可以则设置为 0。
- 回溯法,提供全局变量 ans,以及参数包括数组 masks,位置 pos 和当前状态 mask。
题解:
class Solution {
int ans = 0;
public int maxLength(List<String> arr) {
List<Integer> masks = new ArrayList<Integer>();
for (String s : arr) {
int mask = 0;
for (int i = 0; i < s.length(); ++i) {
int ch = s.charAt(i) - 'a';
if (((mask >> ch) & 1) != 0) { // 若 mask 已有 ch,则说明 s 含有重复字母,无法构成可行解
mask = 0;
break;
}
mask |= 1 << ch; // 将 ch 加入 mask 中
}
if (mask > 0) {
masks.add(mask);
}
}
backtrack(masks, 0, 0);
return ans;
}
public void backtrack(List<Integer> masks, int pos, int mask) {
if (pos == masks.size()) {
ans = Math.max(ans, Integer.bitCount(mask));
return;
}
if ((mask & masks.get(pos)) == 0) { // mask 和 masks[pos] 无公共元素
backtrack(masks, pos + 1, mask | masks.get(pos));
}
backtrack(masks, pos + 1, mask);
}
}60. 剑指 Offer 38. 字符串的排列
参考题解:剑指 Offer 38. 字符串的排列(回溯法,清晰图解)
题目:

标签:
- 回溯法。
思路:
- 这道题可以采用回溯法求解。
- 根据字符串排列的特点,考虑深度优先搜索所有排列方案。即通过字符交换,先固定第 11 位字符( nn 种情况)、再固定第 22 位字符( n-1n−1 种情况)、... 、最后固定第 nn 位字符( 11 种情况)。
- 当字符串存在重复字符时,排列方案中也存在重复的排列方案。为排除重复方案,需在固定某位字符时,保证 “每种字符只在此位固定一次” ,即遇到重复字符时不交换,直接跳过。从 DFS 角度看,此操作称为 “剪枝” 。
题解:
class Solution {
List<String> res = new LinkedList<>();
char[] c;
public String[] permutation(String s) {
c = s.toCharArray();
dfs(0);
return res.toArray(new String[res.size()]);
}
void dfs(int x) {
if (x == c.length - 1) {
res.add(String.valueOf(c));
return;
}
HashSet<Character> set = new HashSet<>();
for (int i = x; i < c.length; ++i) {
if (set.contains(c[i])) {
continue;
}
set.add(c[i]);
swap(i, x);
dfs(x + 1);
swap(i, x);
}
}
void swap(int a, int b) {
char temp = c[a];
c[a] = c[b];
c[b] = temp;
}
}61. 第752题. 打开转盘锁
参考题解:官方题解
题目:
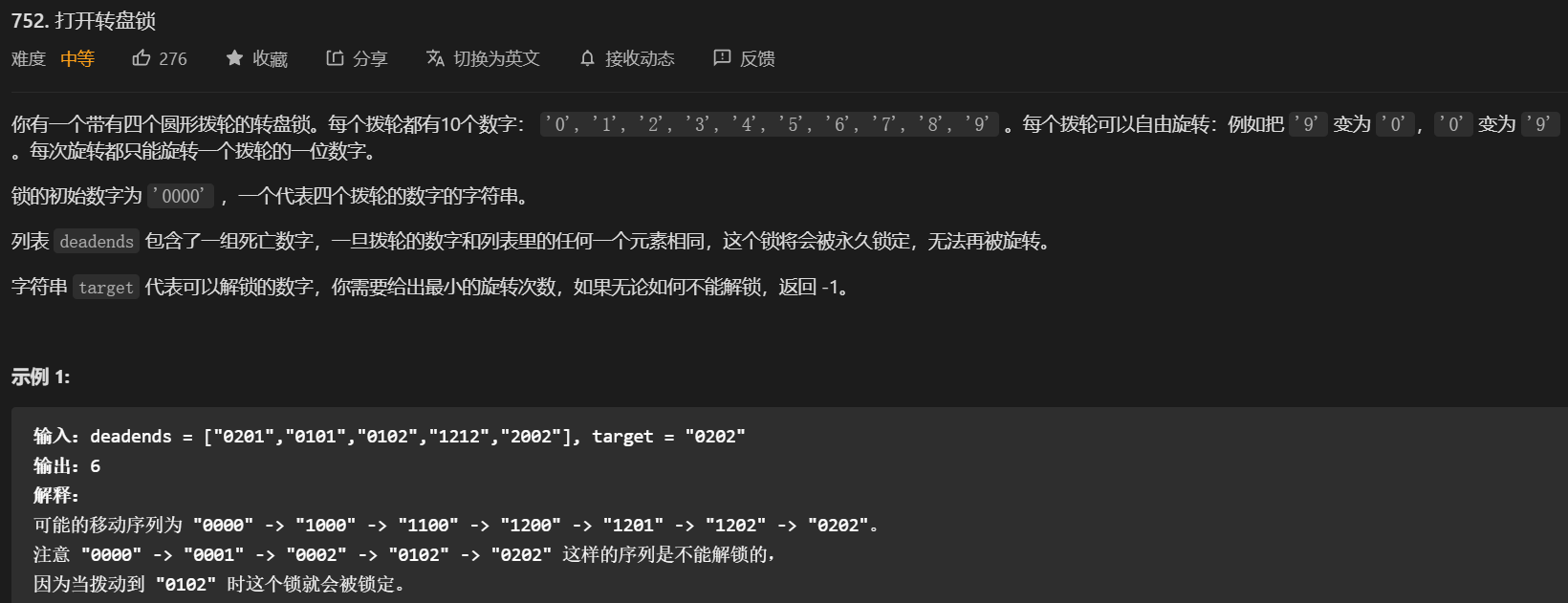
标签:
- 广度优先搜索 BFS。
思路:
- 这道题是一道典型的广度优先搜索。
- 注意,提供给广度优先的是已经访问过的节点,同时要将这个节点送到访问过的集合和将来要访问的队列中。每次提取一个访问队列的内容,获取下一次要访问的列表。所以说访问队列的内容都是访问过的,是为下一次做准备的。
题解:
class Solution {
public int openLock(String[] deadends, String target) {
if ("0000".equals(target)) {
return 0;
}
Set<String> dead = new HashSet<String>();
for (String deadend : deadends) {
dead.add(deadend);
}
if (dead.contains(target)) {
return -1;
}
int step = 0;
Queue<String> queue = new LinkedList<>();
queue.offer("0000");
Set<String> seen = new HashSet<>();
seen.add("0000");
while (!queue.isEmpty()) {
++step;
int size = queue.size();
for (int i = 0; i < size; ++i) {
String status = queue.poll();
for (String nextStatus : get(status)) {
if (!seen.contains(nextStatus) && !dead.contains(nextStatus)) {
if (nextStatus.equals(target)) {
return step;
}
queue.offer(nextStatus);
seen.add(nextStatus);
}
}
}
}
return -1;
}
public char numPrev(char array) {
return (char)((array - '0' + 9) % 10);
}
public char numSucc(char array) {
return (char)((array - '0' + 1) % 10);
}
public List<String> get(String status) {
List<String> res == new ArrayList<>();
char[] array = status.toString();
for (int i = 0; i < 4; ++i) {
char c = array[i];
array[i] = numPrev(array);
res.add(new String(array));
array[i] = numSucc(array);
res.add(new String(array));
array[i] = c;
}
return res;
}
}62. 第279题. 完全平方数
参考题解:官方题解
题目:
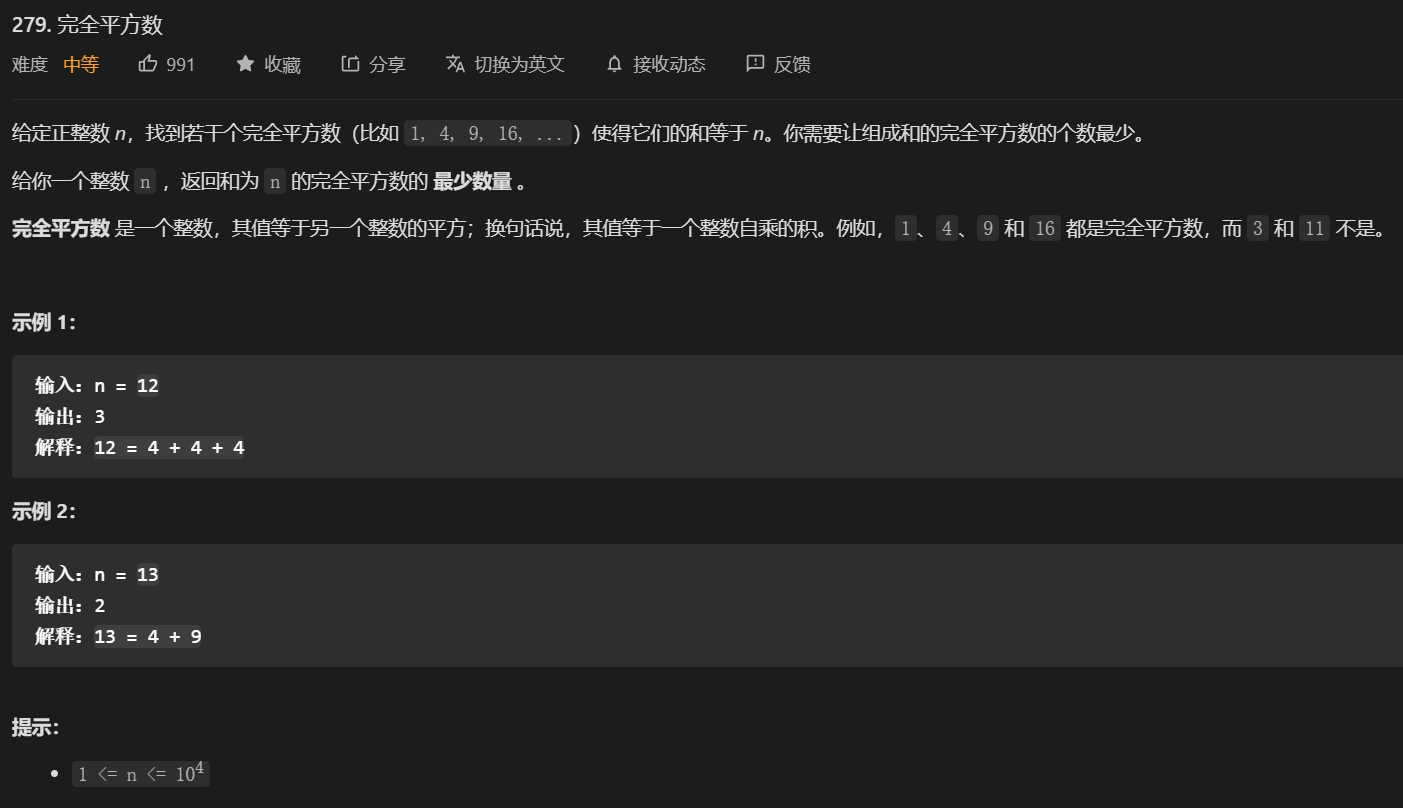
标签:
- 动态规划。
思路:
- 这道题是典型的动态规划。
- 不过,思考起来比较有难度。需要记忆下来这个解法。

题解:
class Solution {
public int numSquares(int n) {
List<Integer> temp = new ArrayList<>();
int[] dp = new int[n + 1];
// 从 1 到 n 遍历
for (int i = 1; i <= n; ++i) {
// 保留每一次遍历的最小值
int min = Integer.MAX_VALUE;
// 从 1 到 j * j <= i 遍历。这里要是 sqrt 可能会有问题,所以这么写
for (int j = 1; j * j <= i; ++j) {
min = Math.min(min, 1 + dp[i - j * j]);
}
dp[i] = min;
}
return dp[n];
}
}63. 第773题. 滑动谜题
参考题解:官方题解
题目:
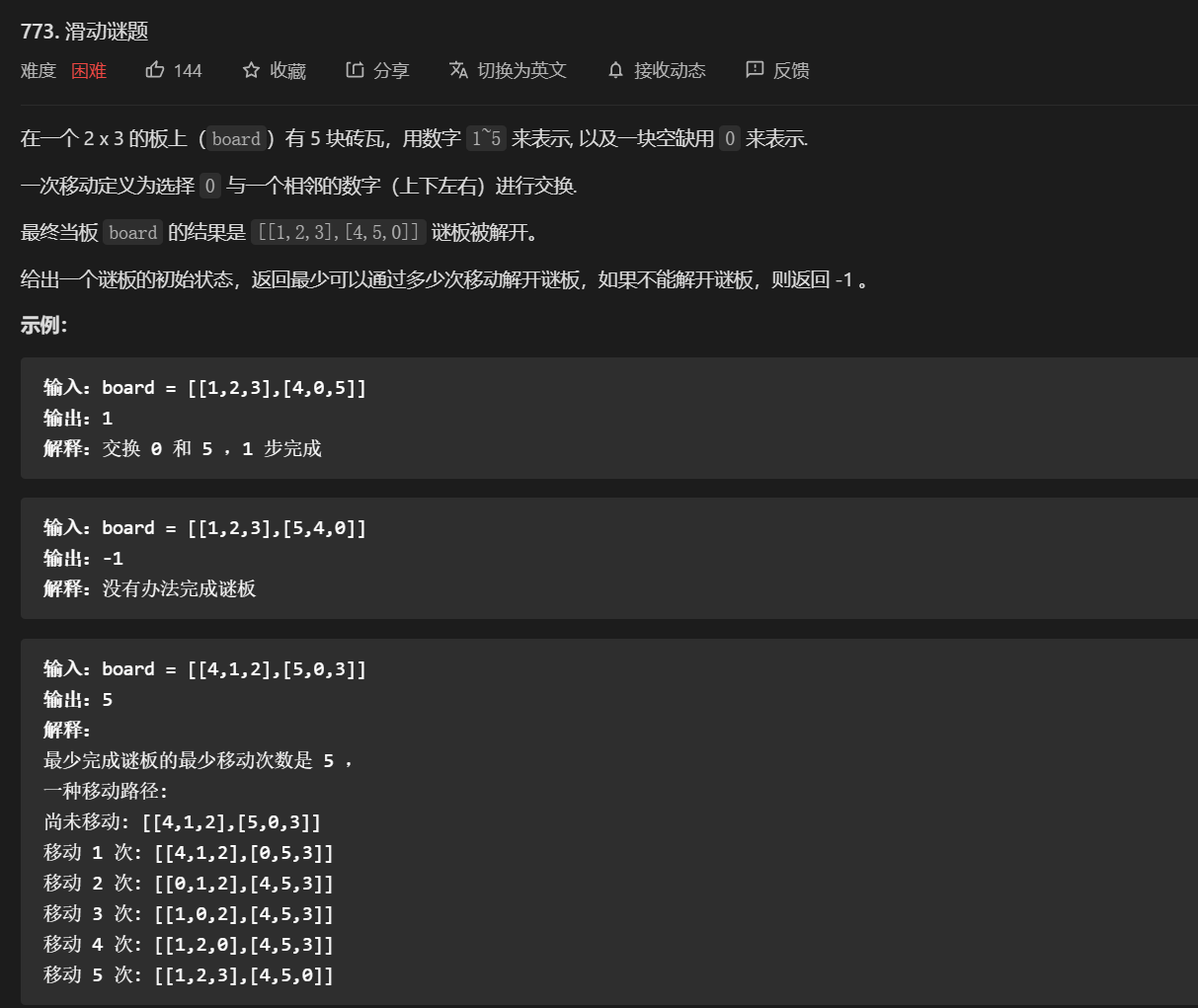
标签:
- 广度优先搜索 BFS。
思路:
-
这道题比较难。我们主要关注 BFS 的模板。
-
int step = 0; Queuequeue = new LinkedList (); queue.offer(initial); Set seen = new HashSet (); seen.add(initial); while (!queue.isEmpty()) { ++step; int size = queue.size(); for (int i = 0; i < size; ++i) { String status = queue.poll(); for (String nextStatus : get(status)) { if (!seen.contains(nextStatus)) { if ("123450".equals(nextStatus)) { return step; } queue.offer(nextStatus); seen.add(nextStatus); } } } }
题解:
class Solution {
int[][] neighbors = {{1, 3}, {0, 2, 4}, {1, 5}, {0, 4}, {1, 3, 5}, {2, 4}};
public int slidingPuzzle(int[][] board) {
StringBuffer sb = new StringBuffer();
for (int i = 0; i < 2; ++i) {
for (int j = 0; j < 3; ++j) {
sb.append(board[i][j]);
}
}
String initial = sb.toString();
if ("123450".equals(initial)) {
return 0;
}
int step = 0;
Queue<String> queue = new LinkedList<String>();
queue.offer(initial);
Set<String> seen = new HashSet<String>();
seen.add(initial);
while (!queue.isEmpty()) {
++step;
int size = queue.size();
for (int i = 0; i < size; ++i) {
String status = queue.poll();
for (String nextStatus : get(status)) {
if (!seen.contains(nextStatus)) {
if ("123450".equals(nextStatus)) {
return step;
}
queue.offer(nextStatus);
seen.add(nextStatus);
}
}
}
}
return -1;
}
// 枚举 status 通过一次交换操作得到的状态
public List<String> get(String status) {
List<String> ret = new ArrayList<String>();
char[] array = status.toCharArray();
int x = status.indexOf('0');
for (int y : neighbors[x]) {
swap(array, x, y);
ret.add(new String(array));
swap(array, x, y);
}
return ret;
}
public void swap(char[] array, int x, int y) {
char temp = array[x];
array[x] = array[y];
array[y] = temp;
}
}64. 第451题. 根据字符出现频率排序
参考题解:[官方题解]()
题目:
标签:
- 桶排序。
思路:
- 这道题可以采用 HashMap 配合 Collections.sort() 进行处理。当然采用 Collections.sort() 也是考察编程技巧的。
- 采用桶排序则是另一种很好的思想。因为频率是有限的,所以可以记录每个频率出现的数字,最后从小到大按照要求输出即可。
- 桶排序方法中,官方题解采用的是 StringBuffer 数组的方法,也是很不错的。节省了空间还降低了时间复杂度。
题解1:HashMap 记录 + Collections.sort() 排序
class Solution {
private HashMap<Character, Integer> map;
public String frequencySort(String s) {
char[] array = s.toCharArray();
map = new HashMap<>();
for (char c : array) {
map.put(c, map.getOrDefault(c, 0) + 1);
}
List<Character> list = new ArrayList<>(map.keySet());
Collections.sort(list, (a, b) -> map.get(b) - map.get(a));
StringBuffer sb = new StringBuffer();
for (int i = 0; i < list.size(); ++i) {
char c = list.get(i);
for (int j = 0; j < map.get(c); ++j) {
sb.append(c);
}
}
return sb.toString();
}
}题解2:桶排序
class Solution {
public String frequencySort(String s) {
Map<Character, Integer> map = new HashMap<Character, Integer>();
int maxFreq = 0;
int length = s.length();
for (int i = 0; i < length; i++) {
char c = s.charAt(i);
int frequency = map.getOrDefault(c, 0) + 1;
map.put(c, frequency);
maxFreq = Math.max(maxFreq, frequency);
}
StringBuffer[] buckets = new StringBuffer[maxFreq + 1];
for (int i = 0; i <= maxFreq; i++) {
buckets[i] = new StringBuffer();
}
for (Map.Entry<Character, Integer> entry : map.entrySet()) {
char c = entry.getKey();
int frequency = entry.getValue();
buckets[frequency].append(c);
}
StringBuffer sb = new StringBuffer();
for (int i = maxFreq; i > 0; i--) {
StringBuffer bucket = buckets[i];
int size = bucket.length();
for (int j = 0; j < size; j++) {
for (int k = 0; k < i; k++) {
sb.append(bucket.charAt(j));
}
}
}
return sb.toString();
}
}65. 第1418题. 点菜展示表
个人题解:题目挺简单,就是有点难
题目:
标签:
- 又臭又长。
思路:
- 这道题考察的点还是蛮多的,最主要是考察了对语言的熟悉程度。
- 最后写出的代码都是又臭又长的。不过也还挺优雅,挺有成就感。
题解:
class Solution {
public List<List<String>> displayTable(List<List<String>> orders) {
HashMap<String, HashMap<String, Integer>> map = new HashMap<>();
HashSet<String> set = new HashSet<>();
for (int i = 0; i < orders.size(); ++i) {
String tableNumber = orders.get(i).get(1), foodItem = orders.get(i).get(2);
HashMap<String, Integer> tempMap = map.getOrDefault(tableNumber, new HashMap<>());
tempMap.put(foodItem, tempMap.getOrDefault(foodItem, 0) + 1);
map.put(tableNumber, tempMap);
set.add(foodItem);
}
List<List<String>> res = new ArrayList<>();
String[] tableNumberArray = new String[map.keySet().size()], foodItemArray = new String[set.size()];
map.keySet().toArray(tableNumberArray);
Arrays.sort(tableNumberArray, (s1, s2) -> (Integer.parseInt(s1) - Integer.parseInt(s2)));
set.toArray(foodItemArray);
Arrays.sort(foodItemArray);
List<String> head = new ArrayList<>();
head.add("Table");
for (String s : foodItemArray) {
head.add(s);
}
res.add(head);
for (String table : tableNumberArray) {
List<String> tableList = new ArrayList<>();
tableList.add(table);
HashMap<String, Integer> tempMap = map.get(table);
for (String food : foodItemArray) {
tableList.add("" + tempMap.getOrDefault(food, 0));
}
res.add(tableList);
}
return res;
}
}66. 第457题. 环形数组是否存在循环
参考题解:官方题解
题目:
标签:
- 双指针。
思路:
- 凡是碰到这种环形的题目,第一时间要想到快慢指针。
- 这道题和第 141 题差不多,都是环形链表。
- 前面路过的点就不用作为初始节点了。这里面是将原数组中前面路过的点的值设置为 0 来避免作为初始节点。
- 注意,当存在负数链表时,这个保证返回值在 0 到 n 中是这样写的:
((i + nums[i]) % n + n) % n;。 - 注意里面判断方向是用相乘大于 0。
题解:
class Solution {
public boolean circularArrayLoop(int[] nums) {
boolean flag = false;
for (int i = 0; i < nums.length; ++i) {
if (nums[i] == 0) {
continue;
}
int slow = i, fast = next(nums, i);
while (nums[slow] * nums[fast] > 0 && nums[slow] * nums[next(nums, fast)] > 0) {
if (slow == fast) {
if (slow != next(nums, slow)) {
return true;
} else {
break;
}
}
slow = next(nums, slow);
fast = next(nums, next(nums, fast));
}
int add = i;
while (nums[add] * nums[next(nums, add)] > 0) {
int temp = add;
add = next(nums, add);
nums[add] = 0;
}
}
return false;
}
public int next(int[] nums, int i) {
int n = nums.length;
return ((i + nums[i]) % n + n) % n;
}
}67. 第264题. 丑数II
参考题解:个人题解
题目:
标签:
- 动态规划。
思路:
- 丑数是一种典型的可以用动态规划求解的问题。
- 一定要牢记这一点。
- 注意,因为有可能有重复数字,所以一定要将主要内容放在 while 循环中,循环条件是当前元素必须得比前面的元素要大。
题解:
class Solution {
public int nthUglyNumber(int n) {
int[] dp = new int[n];
dp[0] = 1;
int p1 = 0, p2 = 0, p3 = 0;
for (int i = 1; i < n; ++i) {
while (dp[i] <= dp[i - 1]) {
dp[i] = Math.min(dp[p1] * 2, dp[p2] * 3);
dp[i] = Math.min(dp[i], dp[p3] * 5);
if (dp[i] == dp[p1] * 2) {
p1++;
} else if (dp[i] == dp[p2] * 3) {
p2++;
} else {
p3++;
}
}
}
return dp[n - 1];
}
}类似的,第313题超级丑数也是一样的解法。
class Solution {
public int nthSuperUglyNumber(int n, int[] primes) {
int[] dp = new int[n], p = new int[primes.length];
dp[0] = 1;
for (int i = 1; i < n; ++i) {
while (dp[i] <= dp[i - 1]) {
dp[i] = Integer.MAX_VALUE;
for (int j = 0; j < primes.length; ++j) {
dp[i] = Math.min(dp[i], dp[p[j]] * primes[j]);
}
for (int j = 0; j < primes.length; ++j) {
if (dp[i] == dp[p[j]] * primes[j]) {
p[j]++;
}
}
}
}
return dp[n - 1];
}
}68. 第516题. 最长回文子序列
参考题解:官方题解
题目:
标签:
- 动态规划。
思路:
- 动态规划,没什么好说的。
- 不过,注意这个是子序列,因此思考上会稍微麻烦一点。
- 可以记住:外层遍历从右往左,内层从左往右。
- 判断指针指向的内容是否相等,相等则
dp[i + 1][j - 1] + 2,不等则为dp[i + 1][j]和dp[i][j - 1]中取大的。
题解:
class Solution {
public int longestPalindromeSubseq(String s) {
int n = s.length();
int[][] dp = new int[n][n];
for (int i = n - 1; i >= 0; --i) {
dp[i][i] = 1;
char c1 = s.charAt(i);
for (int j = i + 1; j < n; ++j) {
char c2 = s.charAt(j);
if (c1 == c2) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
return dp[0][n - 1];
}
}69. 第787题. K站中转内最便宜的航班
个人题解:动态规划求解问题
题目:

标签:
- 动态规划。
思路:
- 这道题是一道典型的动态规划题。看到最便宜航班这类字样就应该判断动态规划,而不是图论类算法。
- 判断这道题是动态规划而不是迪杰斯特拉算法,是一步关键思想。
- 随后需要判断:dp数组是几维?外层是什么?内层是什么?
- 外层根据分析,应该是中转次数。内层则是机场。
- 随后判断dp内容。这里很简单应该都是 Integer.MAX_VALUE 作为基础值。
- 最后一个难点是转移方程怎么写。经过思考后应该是:
dp[i][flights[j][1]] = Math.min(dp[i][flights[j][1]], dp[i - 1][flights[j][0]] + flights[j][2]);
题解:
class Solution {
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
int length = flights.length;
int[][] dp = new int[k + 2][n];
for (int i = 0; i < k + 2; ++i) {
for (int j = 0; j < n; ++j) {
dp[i][j] = Integer.MAX_VALUE;
}
}
dp[0][src] = 0;
for (int i = 1; i < k + 2; ++i) {
for (int j = 0; j < length; ++j) {
if (dp[i - 1][flights[j][0]] != Integer.MAX_VALUE) {
dp[i][flights[j][1]] = Math.min(dp[i][flights[j][1]], dp[i - 1][flights[j][0]] + flights[j][2]);
}
}
}
int min = Integer.MAX_VALUE;
for (int i = 0; i < k + 2; ++i) {
// System.out.println(dp[i][dst]);
if (dp[i][dst] < min) {
min = dp[i][dst];
}
}
return min == Integer.MAX_VALUE ? -1 : min;
}
}70. 第797题. 所有可能的路径
参考题解:官方题解
题目:
标签:
- 深度优先遍历。
思路:
- 这道题思路是很简单的。而且是有向无环图,都不用考虑环了。这种题是面试必须要会的。
- 不过,这道题有一些 Java 语言的语法细节很有意思,如果不熟练可能会吃亏。
- 首先,Deque 的使用。Deque 我个人认为是比 Queue 更好用的类型,就是双端队列,左右两侧都可以添加和删除,实现类有 ArrayDeque 和 LinkedList,方法是 offerFirst、pollFirst、offerLast、pollLast。
- 其次,是 Collections 集合类内部的类型转换。例如 ArrayList 和 ArrayDeque 如何互相转换。可以直接类型强制转换就行,将原内容放到
new 新内容类型<数据类型>(原内容)中的括号里面就可以了。 - 最后,递归可以采用
stack.offerLast(y); dfs(graph, y, n); stack.pollLast();实现。
题解:
class Solution {
List<List<Integer>> ans = new ArrayList<List<Integer>>();
Deque<Integer> stack = new ArrayDeque<Integer>();
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
stack.offerLast(0);
dfs(graph, 0, graph.length - 1);
return ans;
}
public void dfs(int[][] graph, int x, int n) {
if (x == n) {
ans.add(new ArrayList<Integer>(stack));
return;
}
for (int y : graph[x]) {
stack.offerLast(y);
dfs(graph, y, n);
stack.pollLast();
}
}
}71. 第295题. 数据流的中位数
参考题解:官方题解
题目:
标签:
- 优先队列
思路:
- 要不断往数组里面放入新的元素,同时又可能多次查询中位数,那么应该怎样做呢?
- 很容易想到优先队列的方法。但是,优先队列不能快速查询指定位置,应该怎么办呢?
- 因此,这道题采用了一种方法:设置两个优先队列!分别是从大到小和从小到大。

题解:
class MedianFinder {
PriorityQueue<Integer> queMin;
PriorityQueue<Integer> queMax;
public MedianFinder() {
queMin = new PriorityQueue<Integer>((a, b) -> (b - a));
queMax = new PriorityQueue<Integer>((a, b) -> (a - b));
}
public void addNum(int num) {
if (queMin.isEmpty() || num <= queMin.peek()) {
queMin.offer(num);
if (queMax.size() + 1 < queMin.size()) {
queMax.offer(queMin.poll());
}
} else {
queMax.offer(num);
if (queMax.size() > queMin.size()) {
queMin.offer(queMax.poll());
}
}
}
public double findMedian() {
if (queMin.size() > queMax.size()) {
return queMin.peek();
}
return (queMin.peek() + queMax.peek()) / 2.0;
}
}72. 第165题. 比较版本号
参考题解:官方题解
题目:
标签:
- 分割字符串
- 双指针
72.1 分割字符串方法
思路:
- Java 中的分割字符串是这样的:
String[] stringArray = s.split(字符串)。 - 其中,特殊符号需要转义。
\需要写成\\\\.*|之类需要写成\\加上符号。||需要写成\\|\\|
- 之后,要设置为默认值是 0。
- 随后依次比较即可。
题解:
class Solution {
public int compareVersion(String version1, String version2) {
String[] v1 = version1.split("\\.");
String[] v2 = version2.split("\\.");
for (int i = 0; i < v1.length || i < v2.length; ++i) {
int x = 0, y = 0;
if (i < v1.length) {
x = Integer.parseInt(v1[i]);
}
if (i < v2.length) {
y = Integer.parseInt(v2[i]);
}
if (x > y) {
return 1;
}
if (x < y) {
return -1;
}
}
return 0;
}
}72.2 双指针方法
思路:
- 还是默认值设为 0,不过这次是每次结果成 10,然后跳过点号。
题解:
class Solution {
public int compareVersion(String version1, String version2) {
int n = version1.length(), m = version2.length();
int i = 0, j = 0;
while (i < n || j < m) {
int x = 0;
for (; i < n && version1.charAt(i) != '.'; ++i) {
x = x * 10 + version1.charAt(i) - '0';
}
++i; // 跳过点号
int y = 0;
for (; j < m && version2.charAt(j) != '.'; ++j) {
y = y * 10 + version2.charAt(j) - '0';
}
++j; // 跳过点号
if (x != y) {
return x > y ? 1 : -1;
}
}
return 0;
}
}73. 第678题. 有效的括号字符串
参考题解:官方题解
题目:
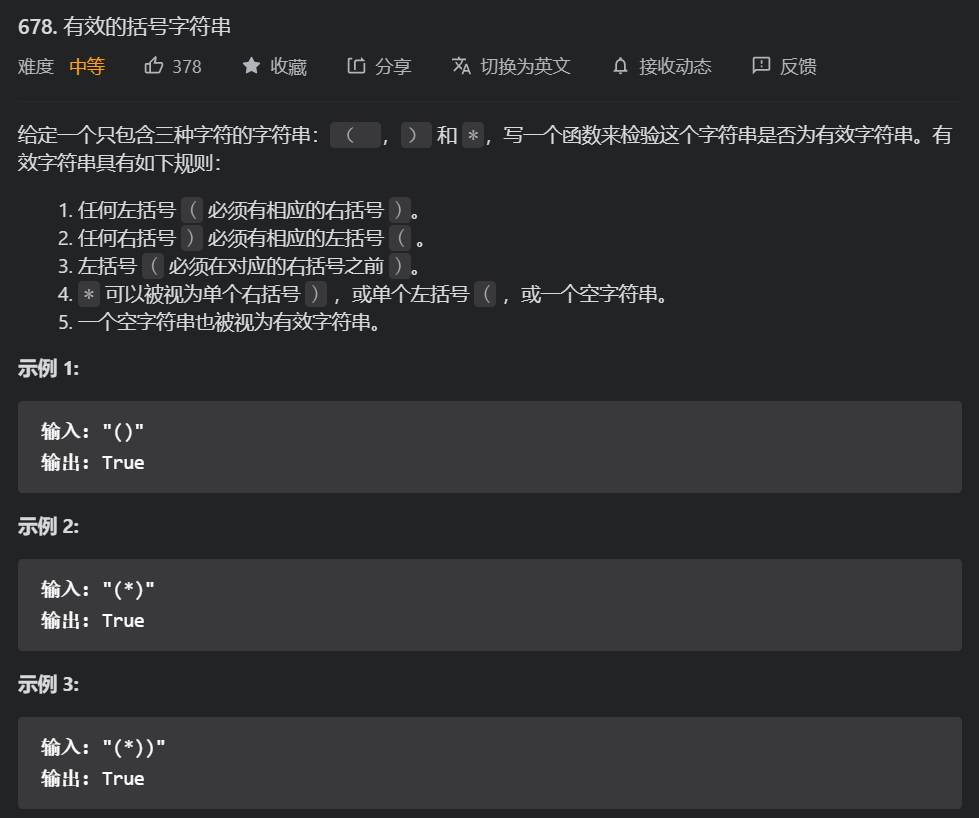
标签:
- 动态规划
- 栈
- 贪心
- 正反遍历
73.1 动态规划求解
思路:
- 这道题的解题方法还是很多的,是很不错的一道题!
- 注意,这道题和一般的括号匹配不同的是,这里有个 * 号,代表的是可以是左括号也可以是右括号。
- 我们设动态规划的条件是:
dp[i][j]是 i 到 j 之间是否是有效字符串。 - 边界条件:长度为 1 时,只有
*才是有效的。长度为 2 时,()、(*、*)、**都是有效的。 - 转移条件:
dp[i + 1][j - 1]为true且s[i] = (,s[j] = )或者均为*,则dp[i][j]为true。另一个转移条件是dp[i][k] 和 dp[k][j]都是true,则dp[i][j]为true。 - 随后就可以用动态规划的方法求解了。这种写法还是难度太大了,不太建议。
题解:
class Solution {
public boolean checkValidString(String s) {
int n = s.length();
boolean[][] dp = new boolean[n][n];
for (int i = 0; i < n; i++) {
if (s.charAt(i) == '*') {
dp[i][i] = true;
}
}
for (int i = 1; i < n; i++) {
char c1 = s.charAt(i - 1), c2 = s.charAt(i);
dp[i - 1][i] = (c1 == '(' || c1 == '*') && (c2 == ')' || c2 == '*');
}
for (int i = n - 3; i >= 0; i--) {
char c1 = s.charAt(i);
for (int j = i + 2; j < n; j++) {
char c2 = s.charAt(j);
if ((c1 == '(' || c1 == '*') && (c2 == ')' || c2 == '*')) {
dp[i][j] = dp[i + 1][j - 1];
}
for (int k = i; k < j && !dp[i][j]; k++) {
dp[i][j] = dp[i][k] && dp[k + 1][j];
}
}
}
return dp[0][n - 1];
}
}73.2 栈求解
思路:
- 这个思路是我最开始考虑的。但我考虑的是:仅仅维护栈元素的话,是不是两个
int类型就够了?这个思路的问题是:只能保证)的正确匹配,而无法保证最后的(和*的正确匹配。因为无法确定(和*的位置! - 修改:用两个真正的栈,分别记录
(和*的下标。 - 另外,这里的栈推荐用
Deque的LinkedList实现,这种方法比较常用。
题解:
class Solution {
public boolean checkValidString(String s) {
Deque<Integer> leftStack = new LinkedList<Integer>();
Deque<Integer> asteriskStack = new LinkedList<Integer>();
int n = s.length();
for (int i = 0; i < n; i++) {
char c = s.charAt(i);
if (c == '(') {
leftStack.push(i);
} else if (c == '*') {
asteriskStack.push(i);
} else {
if (!leftStack.isEmpty()) {
leftStack.pop();
} else if (!asteriskStack.isEmpty()) {
asteriskStack.pop();
} else {
return false;
}
}
}
while (!leftStack.isEmpty() && !asteriskStack.isEmpty()) {
int leftIndex = leftStack.pop();
int asteriskIndex = asteriskStack.pop();
if (leftIndex > asteriskIndex) {
return false;
}
}
return leftStack.isEmpty();
}
}73.3 贪心求解
思路:
- 这种思路也是和栈的方法比较类似,但是有一点不太好想。
- 由于
*可以代表两种括号,所以我们可以设置max和min来分别代表左括号的最大值和最小值。 - 遇到左括号,则两个都加一。遇到右括号,则两个都减一,注意
min小于 0 应该设为 0,同时如果max < 0,则返回不能。遇到*则min还是减一,同样最小应该设为 0,max则相应加一。 - 最后出来,只有
min为 0 时才是有效的字符串。
题解:
class Solution {
public boolean checkValidString(String s) {
int minCount = 0, maxCount = 0;
int n = s.length();
for (int i = 0; i < n; i++) {
char c = s.charAt(i);
if (c == '(') {
minCount++;
maxCount++;
} else if (c == ')') {
minCount = Math.max(minCount - 1, 0);
maxCount--;
if (maxCount < 0) {
return false;
}
} else {
minCount = Math.max(minCount - 1, 0);
maxCount++;
}
}
return minCount == 0;
}
}73.4 两次遍历法
思路:
- 这个思路同样很好,以后可以借鉴。这差不多是最简单的方法。
- 左边往右边扫描,保证右括号有左括号。右边往左边扫描,保证左括号有右括号。
题解:
class Solution {
public boolean checkValidString(String s) {
int left = 0, right = 0, val = 0;
char[] charArray = s.toCharArray();
for (char c : charArray) {
if (c == '(') {
++left;
} else if (c == '*') {
++val;
} else {
if (left != 0) {
--left;
} else if (val != 0) {
--val;
} else {
return false;
}
}
}
left = 0;
right = 0;
val = 0;
for (int i = charArray.length - 1; i >= 0; --i) {
char c = charArray[i];
if (c == ')') {
++right;
} else if (c == '*') {
++val;
} else {
if (right != 0) {
--right;
} else if (val != 0) {
--val;
} else {
return false;
}
}
}
return true;
}
}74. 面试题17.10. 主要元素
参考题解:官方题解
题目:
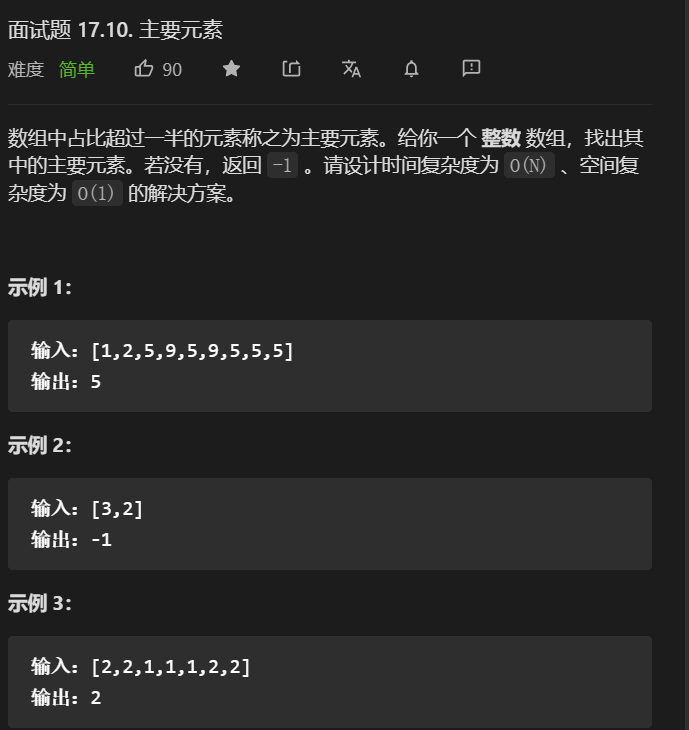
标签:
- 意想不到。
思路:
- 要求 O(n) 时间找到占比超过一半的元素,且 O(1) 空间复杂度。
- 这只有一种算法:
Boyer-Moore投票算法。 - 维护一个主要元素
candidate和次数count,第一次遍历用于找到主要元素,第二次遍历用于确认是否是真的主要元素。 - 第一次遍历,如果
count为 0 则用当前元素替代,否则如果当前元素和candidate相等则count + 1否则count - 1。 - 第二次遍历判断 candidate 是否超过半数即可。用
Math.floor()比较好。
题解:
class Solution {
public int majorityElement(int[] nums) {
int length = nums.length, res = -1;
int count = 0, candidate = -1;
for (int i : nums) {
if (count == 0) {
count = 1;
candidate = i;
} else if (i != candidate) {
count --;
} else {
count ++;
}
}
count = 0;
for (int i : nums) {
if (i == candidate) {
count ++;
if (count > Math.floor((double)length / 2)) {
res = candidate;
break;
}
}
}
return res;
}
}75. 面试题 10.02 变位数组
个人题解:HashMap 求解问题
题目:
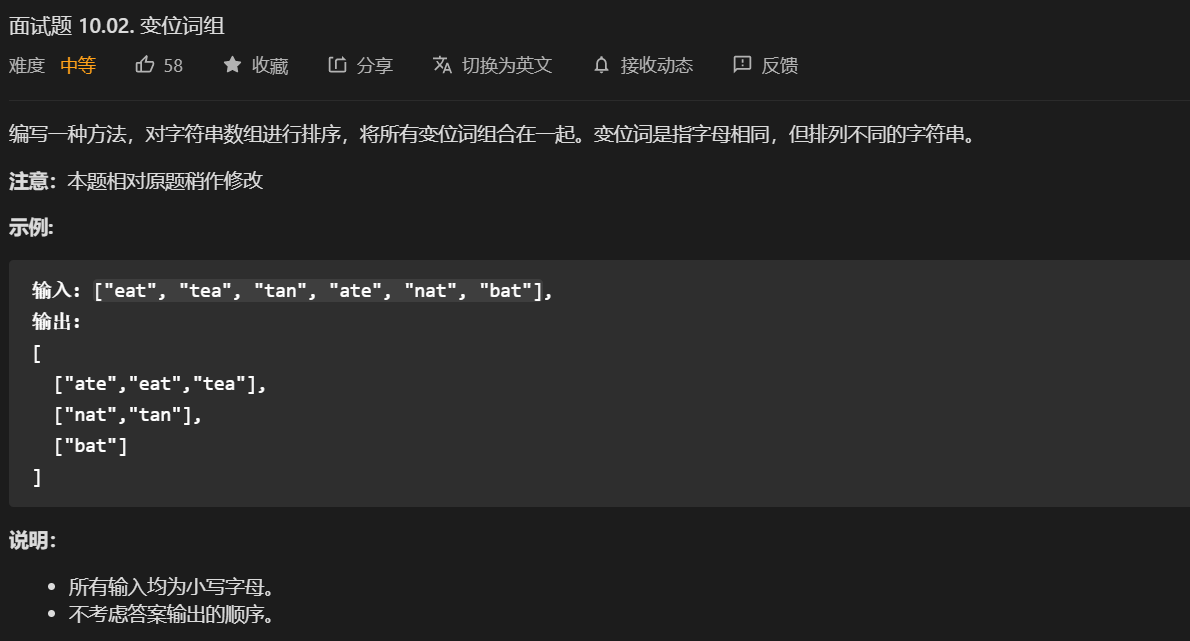
标签:
- 考研编码。
思路:
- 这道题没什么难点。
- 首先构建一个数组,将所有原数组的字符串按照字符进行排序,得到一个标准字符串列表。
- 随后构建 HashMap,存储标准字符串和在结果数组中的位置。
- 最后在结果数组中构建答案即可。
题解:
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
List<List<String>> res = new ArrayList<>();
if (strs.length == 0) {
return res;
}
String[] map = new String[strs.length];
for (int i = 0; i < strs.length; ++i) {
char[] array = strs[i].toCharArray();
Arrays.sort(array);
map[i] = new String(array);
}
HashMap<String, Integer> hashMap = new HashMap<>();
for (int i = 0; i < strs.length; ++i) {
if (hashMap.containsKey(map[i])) {
int val = hashMap.get(map[i]);
List<String> temp = res.get(val);
temp.add(strs[i]);
res.set(val, temp);
} else {
int val = hashMap.size();
hashMap.put(map[i], val);
List<String> temp = new ArrayList<>();
temp.add(strs[i]);
res.add(temp);
}
}
return res;
}
}76. 第1838题. 最高频元素的频数
参考题解:官方题解
题目:
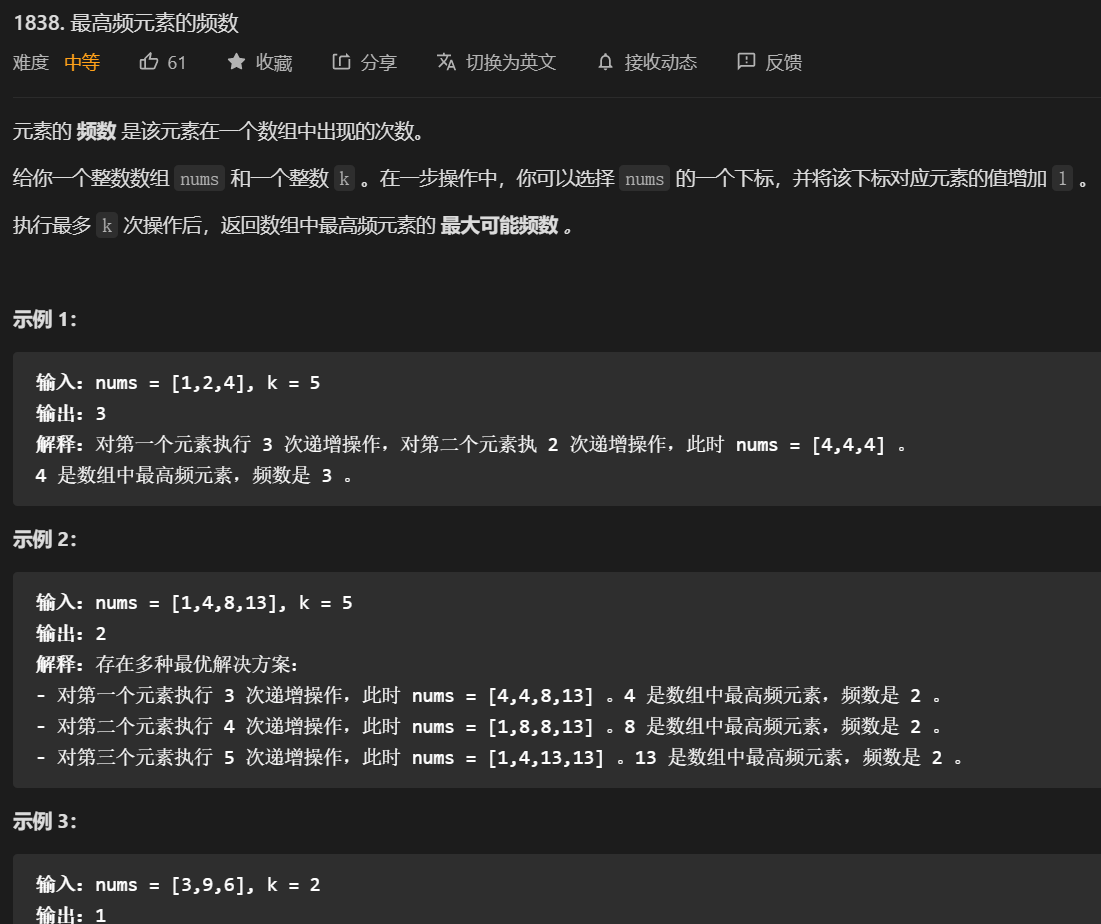
标签:
-
模板题。
-
滑动窗口。
思路:
- 首先需要对数组进行排序,随后使用滑动窗口即可。
- 注意 total 的计算,要用
(nums[r] - nums[r - 1]) * (r - l)。 - 不满足条件时,减少
nums[r] - nums[l],然后左指针加一即可。不需要更复杂的操作。
题解:
class Solution {
public int maxFrequency(int[] nums, int k) {
Arrays.sort(nums);
int n = nums.length;
long total = 0;
int l = 0, res = 1;
for (int r = 1; r < n; ++r) {
total += (long) (nums[r] - nums[r - 1]) * (r - l);
while (total > k) {
total -= nums[r] - nums[l];
++l;
}
res = Math.max(res, r - l + 1);
}
return res;
}
}77. 第300题. 最长递增子序列
参考题解:官方题解
题目:
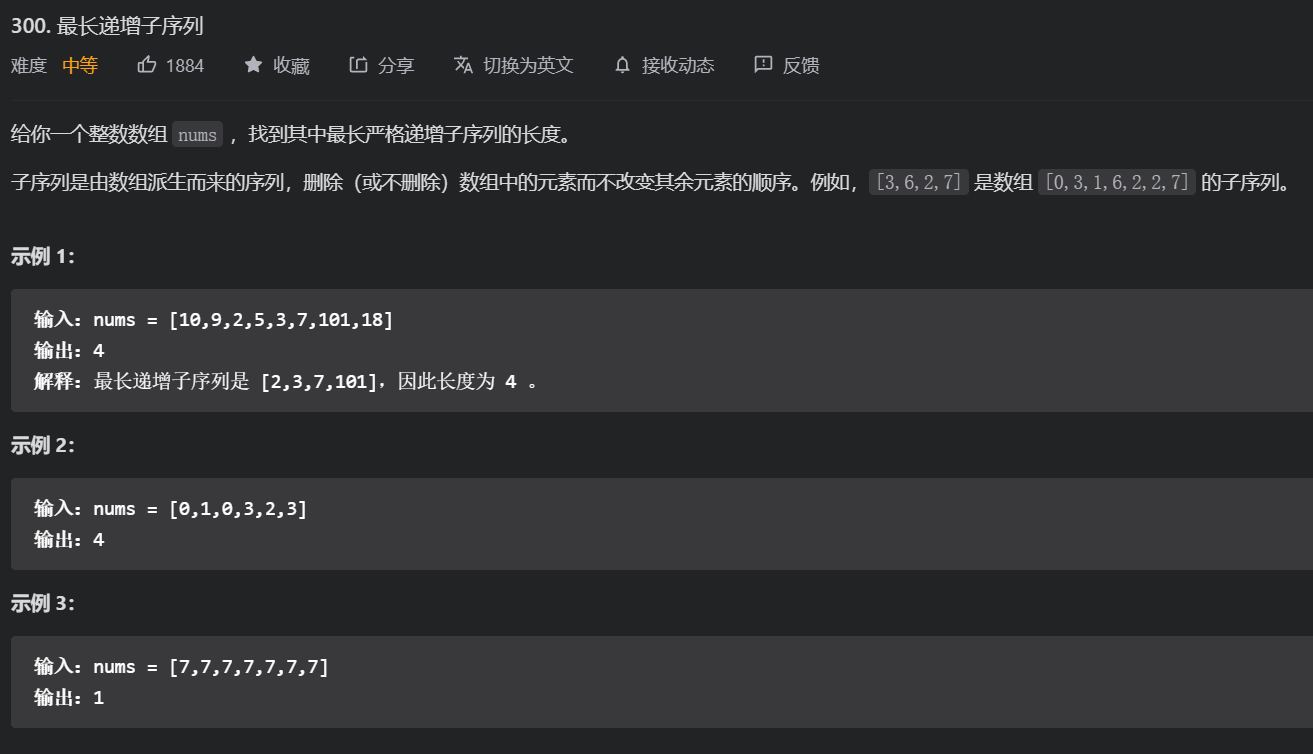
标签:
- 动态规划
思路:
- 太久没做这道题了,还是需要复习一下。
- 最长递增子序列的时间复杂度是 O(n^2),这个要记住。只要记住没有更好的时间复杂度的算法,基本就能想到完整的思路,问题也就迎刃而解了。
题解:
class Solution {
public int lengthOfLIS(int[] nums) {
int n = nums.length, max = 0;
int[] dp = new int[n];
if (n == 0) {
return max;
}
dp[0] = 1;
max = 1;
for (int i = 1; i < nums.length; ++i) {
int tempMax = 0;
for (int j = 0; j < i; ++j) {
if (nums[i] > nums[j] && dp[j] > tempMax) {
tempMax = dp[j];
}
}
dp[i] = tempMax + 1;
if (dp[i] > max) {
max = dp[i];
}
}
return max;
}
}78. 第673题. 最长递增子序列的个数
参考题解:官方题解
题目:
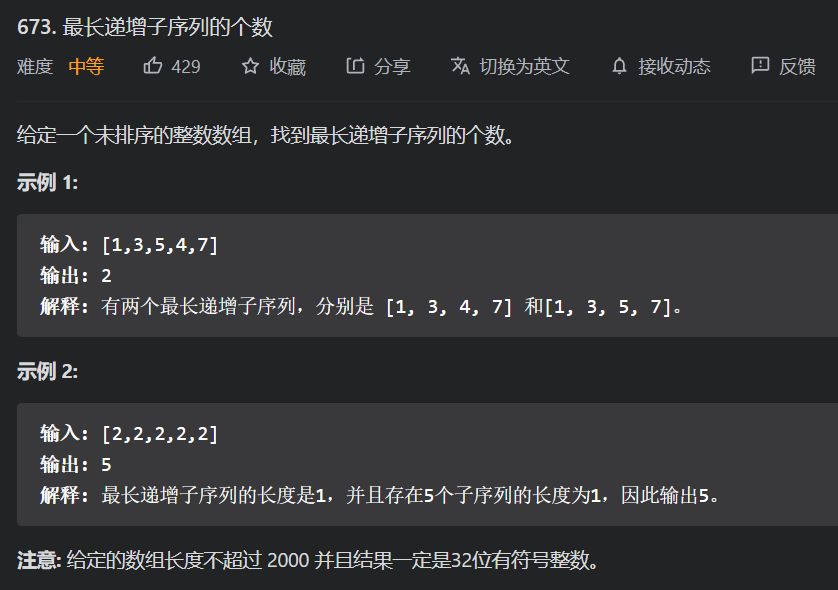
标签:
- 动态规划
思路:
- 这道题其实挺难的,我认为比 300 题最长递归子序列难一个等级。
- 首先,需要再构建一个 count 数组,记录达到当前最长递增子序列的数量。
- 注意,当认为当前序列是目前的最长递增子序列时,如果是新发现的序列,就需要更新 count;如果是和前面一样长的,就需要加上这个的 count 长度,注意不是加一,而是加这个 count 长度。
- 随后,如果认为当前是新的最长子序列,就需要更新 max 和 res;如果是和前面一样长的子序列,就需要更新 res。
题解:
class Solution {
public int findNumberOfLIS(int[] nums) {
int n = nums.length, max = 0, res = 0;
if (n == 0) {
return 0;
}
int[] dp = new int[n];
int[] count = new int[n];
for (int i = 0; i < n; ++i) {
dp[i] = 1;
count[i] = 1;
for (int j = 0; j < i; ++j) {
if (nums[i] > nums[j]) {
if (dp[j] + 1 > dp[i]) {
dp[i] = dp[j] + 1;
count[i] = count[j];
} else if (dp[j] + 1 == dp[i]) {
count[i] += count[j];
}
}
} if (dp[i] > max) {
max = dp[i];
res = count[i];
} else if (dp[i] == max) {
res += count[i];
}
}
return res;
}
}79. 第650题. 只有两个键的键盘
参考题解:[官方题解]()
题目:
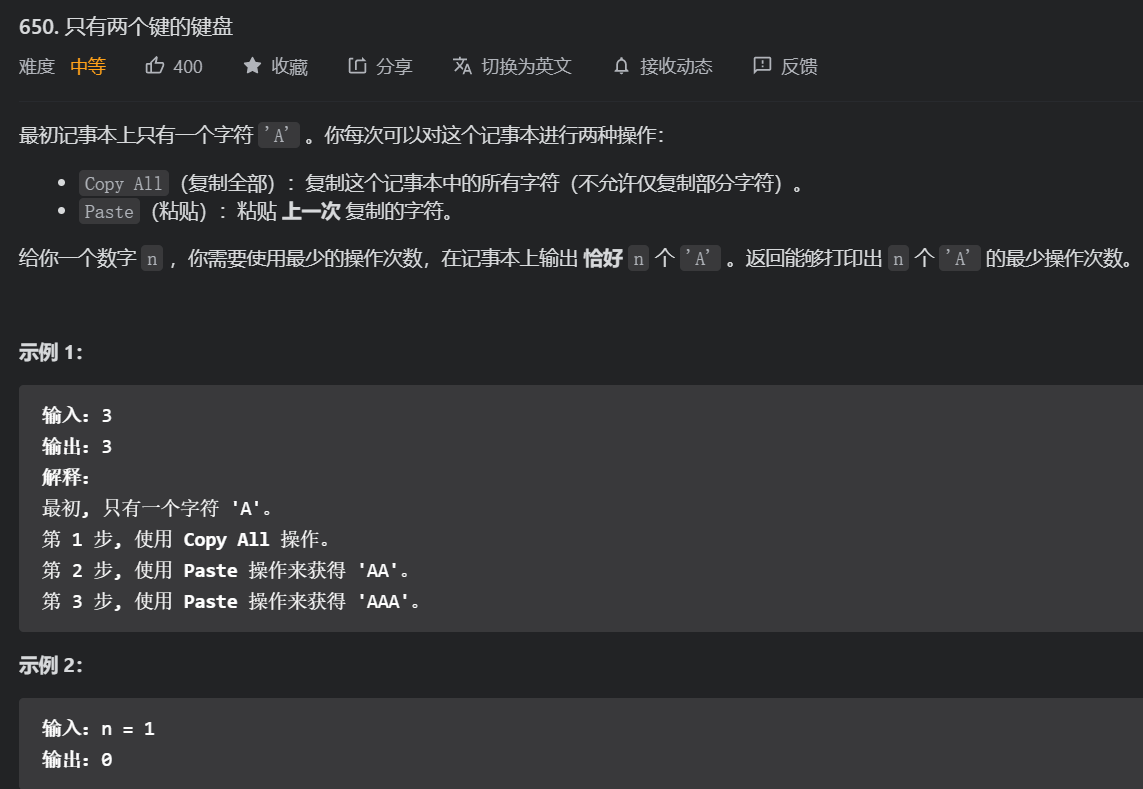
标签:
- 动态规划
思路:
- 这道题是道很不错的动态规划!建议多刷几次。
- 就是找目标值的因子,然后从低到高遍历,最后找到
dp[n]的值。由于目标是找到最小的动作次数,所以每次都要找最小值。 - 因为是找因子,所以二层遍历可以在平方小于目标值的情况下查找,降低时间复杂度。
- 转移方程就是,看
i / j + dp[j]和dp[i / j] + j还有dp[i]哪个小。目标是找到这个 i 对应的最小的dp[i],所以需要两个Math.min。
题解:
class Solution {
public int minSteps(int n) {
int[] dp = new int[n + 1];
for (int i = 2; i <= n; ++i) {
dp[i] = Integer.MAX_VALUE;
for (int j = 1; j * j <= i; ++j) {
if (i % j == 0) {
dp[i] = Math.min(dp[i], i / j + dp[j]);
dp[i] = Math.min(dp[i], dp[i / j] + j);
}
}
}
return dp[n];
}
}80. 第430题. 扁平化多级双向链表
参考题解:官方题解
题目:
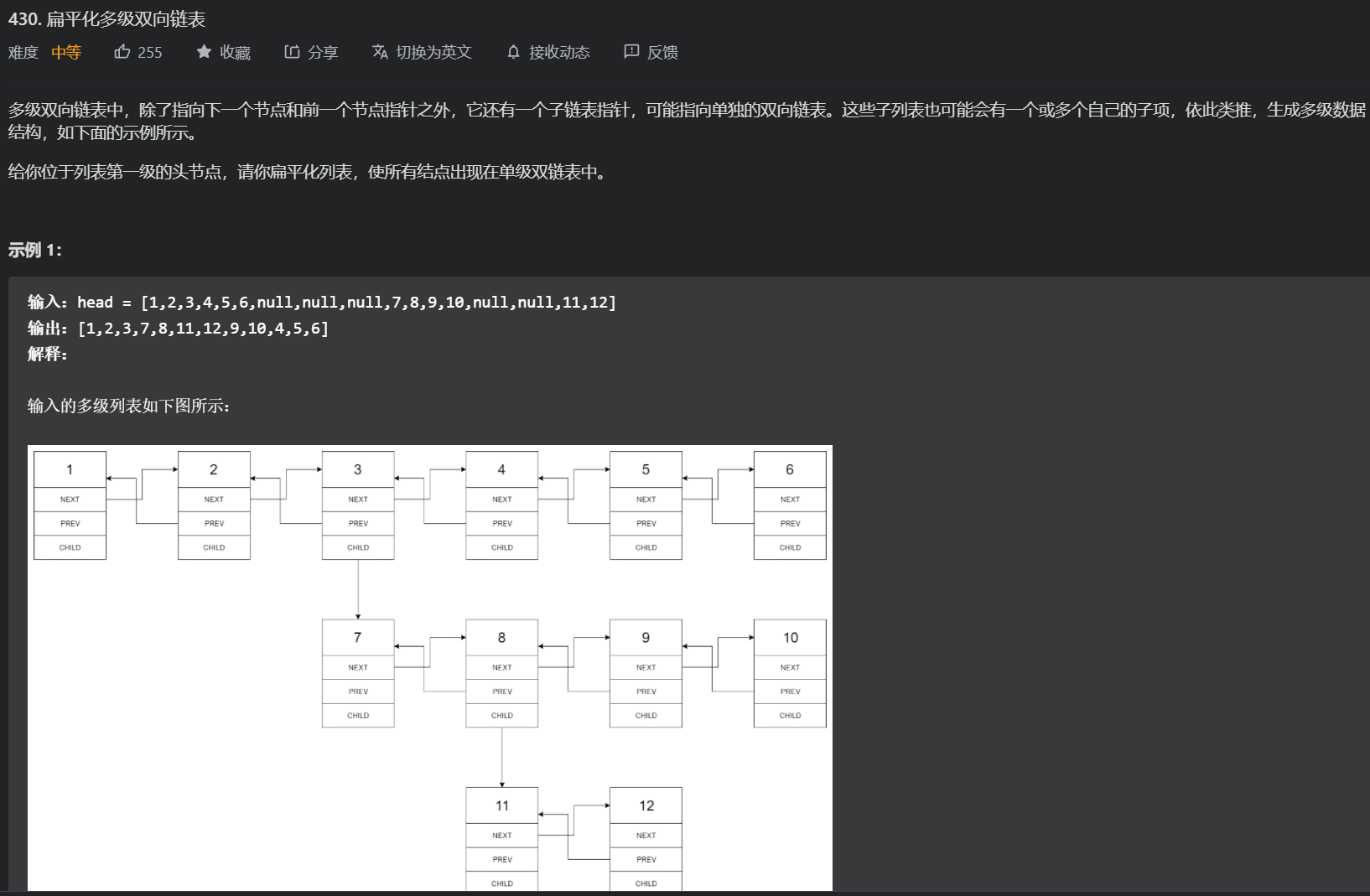
标签:
- 链表
思路:
- 这道题还是挺难的,得多思考思考。
题解:
class Solution {
public Node flatten(Node head) {
dfs(head);
return head;
}
public Node dfs(Node node) {
Node cur = node;
// 记录链表的最后一个节点
Node last = null;
while (cur != null) {
Node next = cur.next;
// 如果有子节点,那么首先处理子节点
if (cur.child != null) {
Node childLast = dfs(cur.child);
next = cur.next;
// 将 node 与 child 相连
cur.next = cur.child;
cur.child.prev = cur;
// 如果 next 不为空,就将 last 与 next 相连
if (next != null) {
childLast.next = next;
next.prev = childLast;
}
// 将 child 置为空
cur.child = null;
last = childLast;
} else {
last = cur;
}
cur = next;
}
return last;
}
}81. 第371题. 两整数之和
参考题解:官方题解
题目:
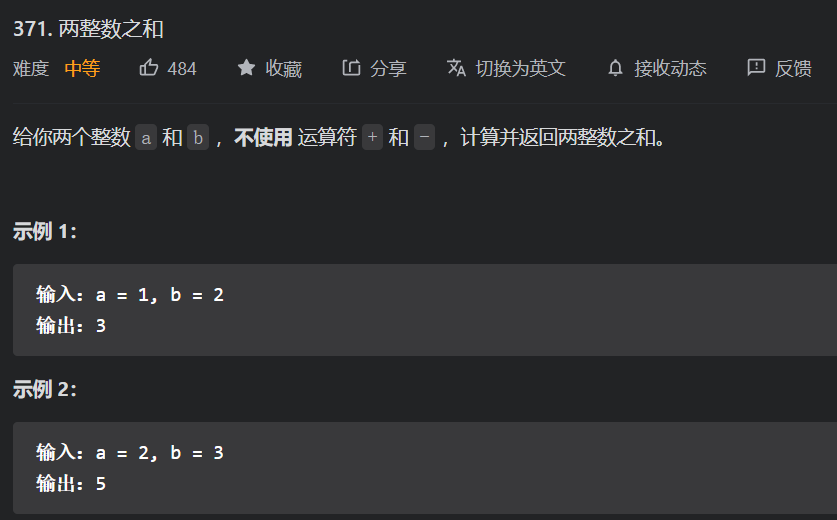
标签:
- 位运算
- 意想不到
- 必考
思路:
- 这道题可以说是必考了,非常重要。
- 题目要求是:不使用加和减运算符,求解 a + b。
- 方法自然是位运算。但是,怎么进行位运算呢?
- 考虑到二进制 0 + 0 = 0, 1 + 0 = 0 + 1 = 1,1 + 1 = 0,因此有 a + b 的进位是 a & b,不考虑进位是 a ^ (异或) b,进位结果是 (a & b) << 1。
- 当然,另一种简单方法是调用 Integer.sum() 方法哦~
题解:
class Solution {
public int getSum(int a, int b) {
while (b != 0) {
int carry = (a & b) << 1;
a = a ^ b;
b = carry;
}
return a;
}
}82. 第437题. 路径总和 III
个人题解:深度遍历+前缀和求解问题
题目:
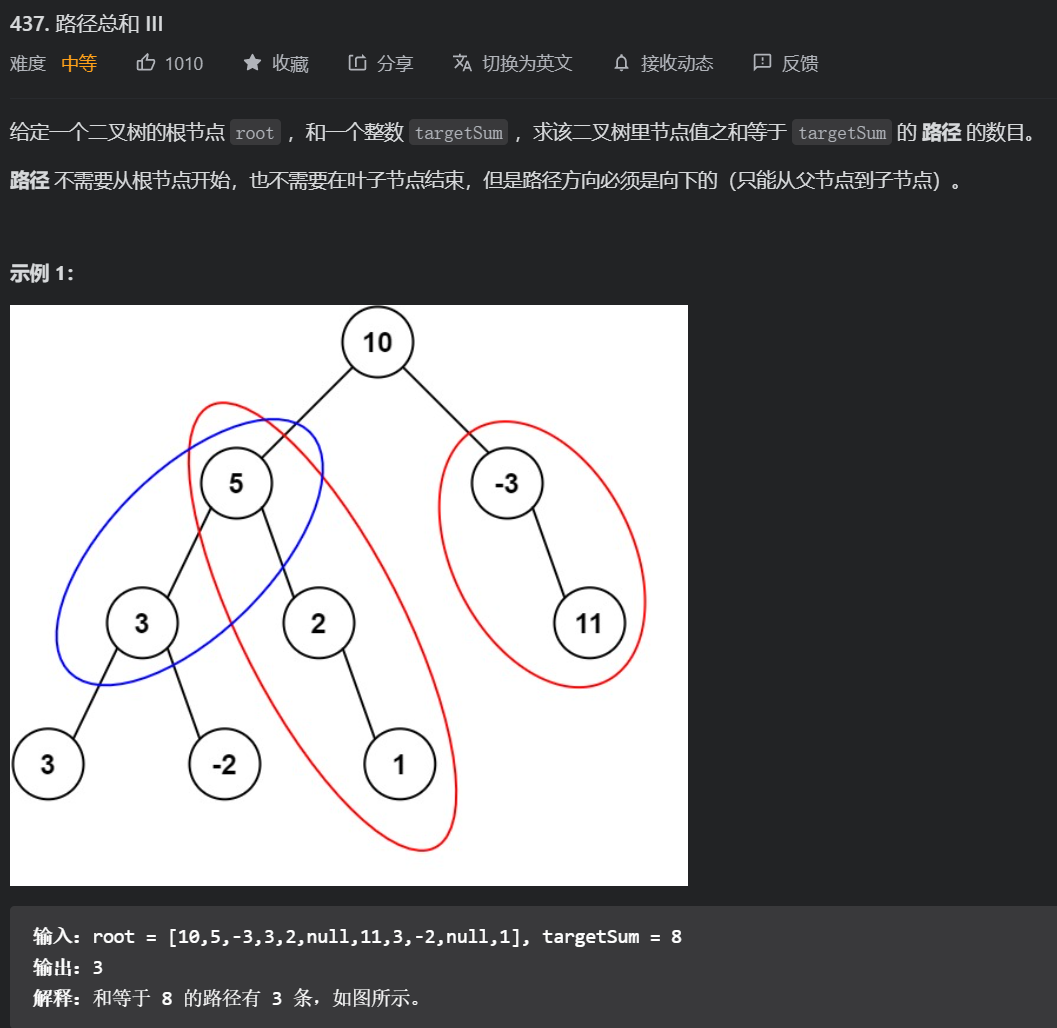
标签:
- 深度遍历
- 前缀和
思路:
- 首先,这个问题很明显是深度遍历+前缀和,但是,写的时候容易出问题。
- 首先,需要用 HashMap,因为前缀一致的可能有很多个,我们要保留所有路径。
- 其次,要先更新 count,然后再 put。如果顺序反了,会造成结果错误。
题解:
class Solution {
int count;
int target;
public int pathSum(TreeNode root, int targetSum) {
HashMap<Integer, Integer> map = new HashMap<>();
map.put(0, 1);
this.target = targetSum;
dp(map, root, 0);
return this.count;
}
public void dp(HashMap<Integer, Integer> map, TreeNode node, int sum) {
if (node == null) {
return;
} else {
sum += node.val;
if (map.get(sum - this.target) != null) {
this.count += map.get(sum - this.target);
// System.out.printf("%d, %d\n", sum, sum - target);
}
map.put(sum, map.getOrDefault(sum, 0) + 1);
if (node.left != null) {
HashMap<Integer, Integer> mapLeft = new HashMap<>(map);
dp(mapLeft, node.left, sum);
}
if (node.right != null) {
HashMap<Integer, Integer> mapRight = new HashMap<>(map);
dp(mapRight, node.right, sum);
}
}
}
}83. 第517题. 超级洗衣机
参考题解:官方题解
题目:
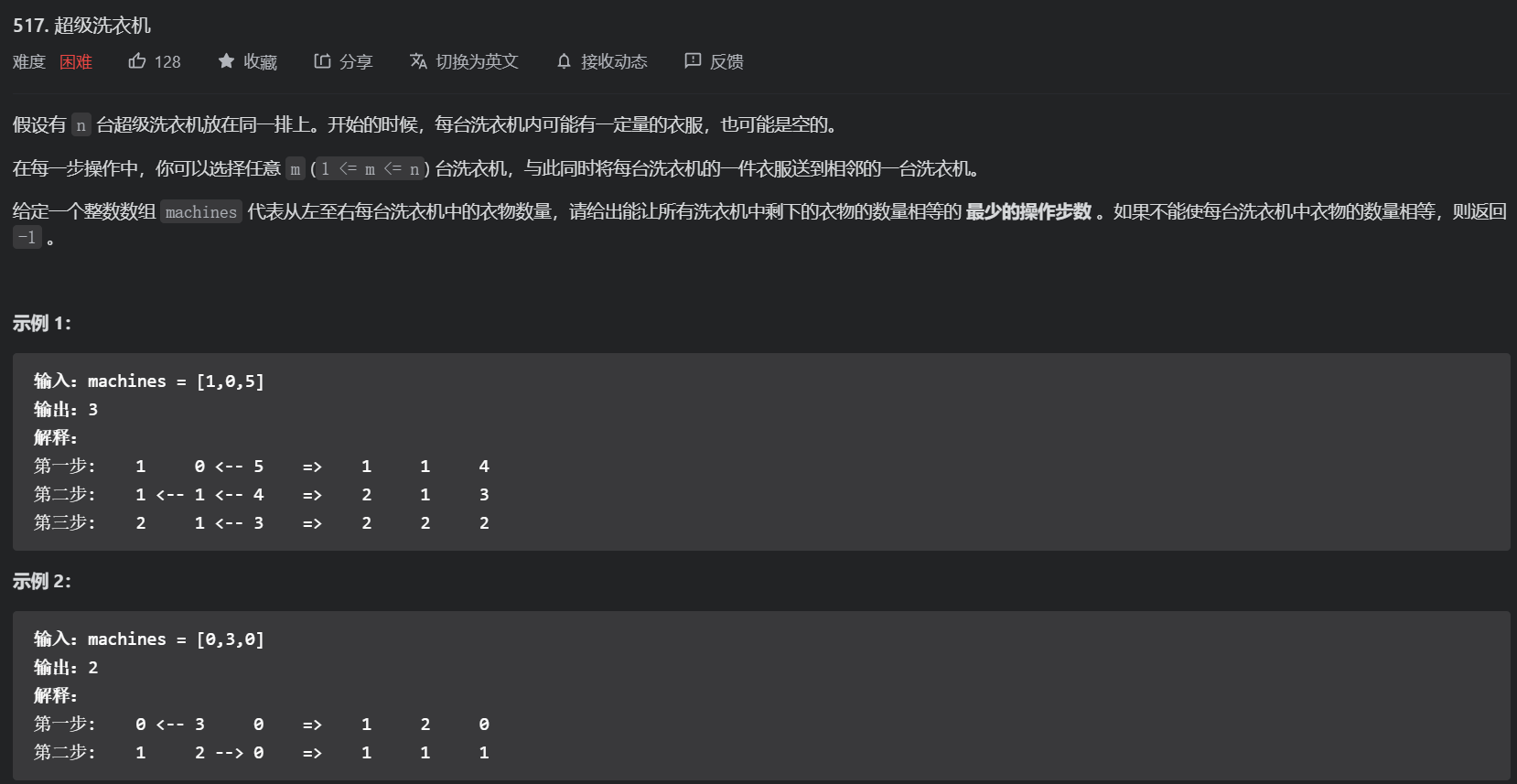
标签:
-
贪心
-
数学
-
恶心
思路:
- 其实很好看出来这个是贪心法。但是!一定要注意,不是移动一步总和就加一,而是所有需要移动的内容向旁边移动一步,才加一。
- 因此,这个求结果就不能简单的求和了,而是要求需要移动的最大值!
- 这个最大值需要考虑:将目标值移动成平均值时的移动次数,以及左右移动值的移动次数。这两个中取最大的就可以了。
题解:
class Solution {
public int findMinMoves(int[] machines) {
int tot = Arrays.stream(machines).sum();
int n = machines.length;
if (tot % n != 0) {
return -1;
}
int avg = tot / n;
int ans = 0, sum = 0;
for (int num : machines) {
num -= avg;
sum += num;
ans = Math.max(ans, Math.max(Math.abs(sum), num));
}
return ans;
}
}84. 第223题. 矩形面积
个人题解:数组排序求解问题
题目:
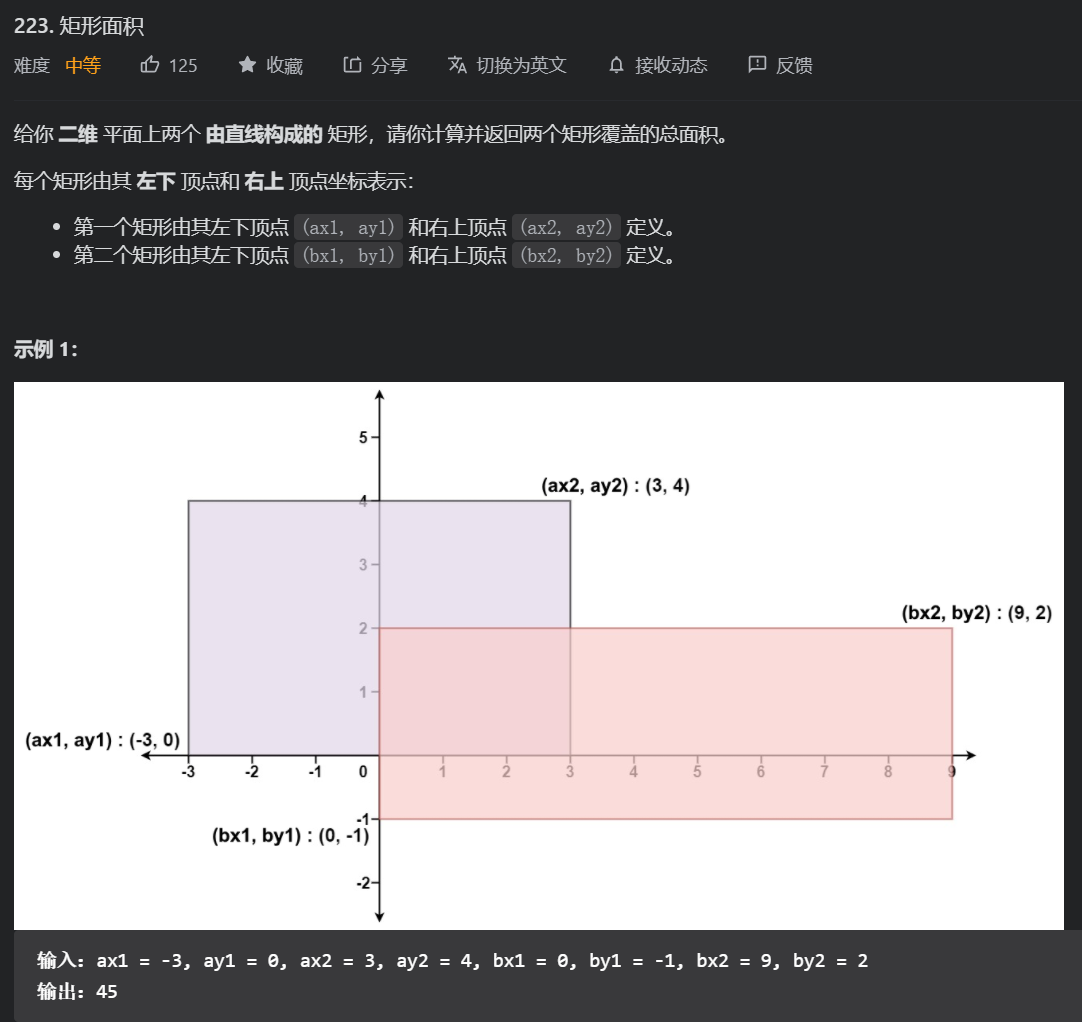
标签:
- 必考
思路:
- 比较简单的一道题,但是仍然考验思路。
题解:
class Solution {
public int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
int[] x = new int[]{ax1, ax2, bx1, bx2};
int[] y = new int[]{ay1, ay2, by1, by2};
int res = 0;
Arrays.sort(x);
Arrays.sort(y);
res = (ax2 - ax1) * (ay2 - ay1) + (bx2 - bx1) * (by2 - by1);
if (!((ax1 > bx2) || (ax2 < bx1) || (ay1 > by2) || (ay2 < by1))) {
res -= (x[2] - x[1]) * (y[2] - y[1]);
}
return res;
}
}85. 第405题. 数字转换为十六进制数
参考题解:官方题解
题目:
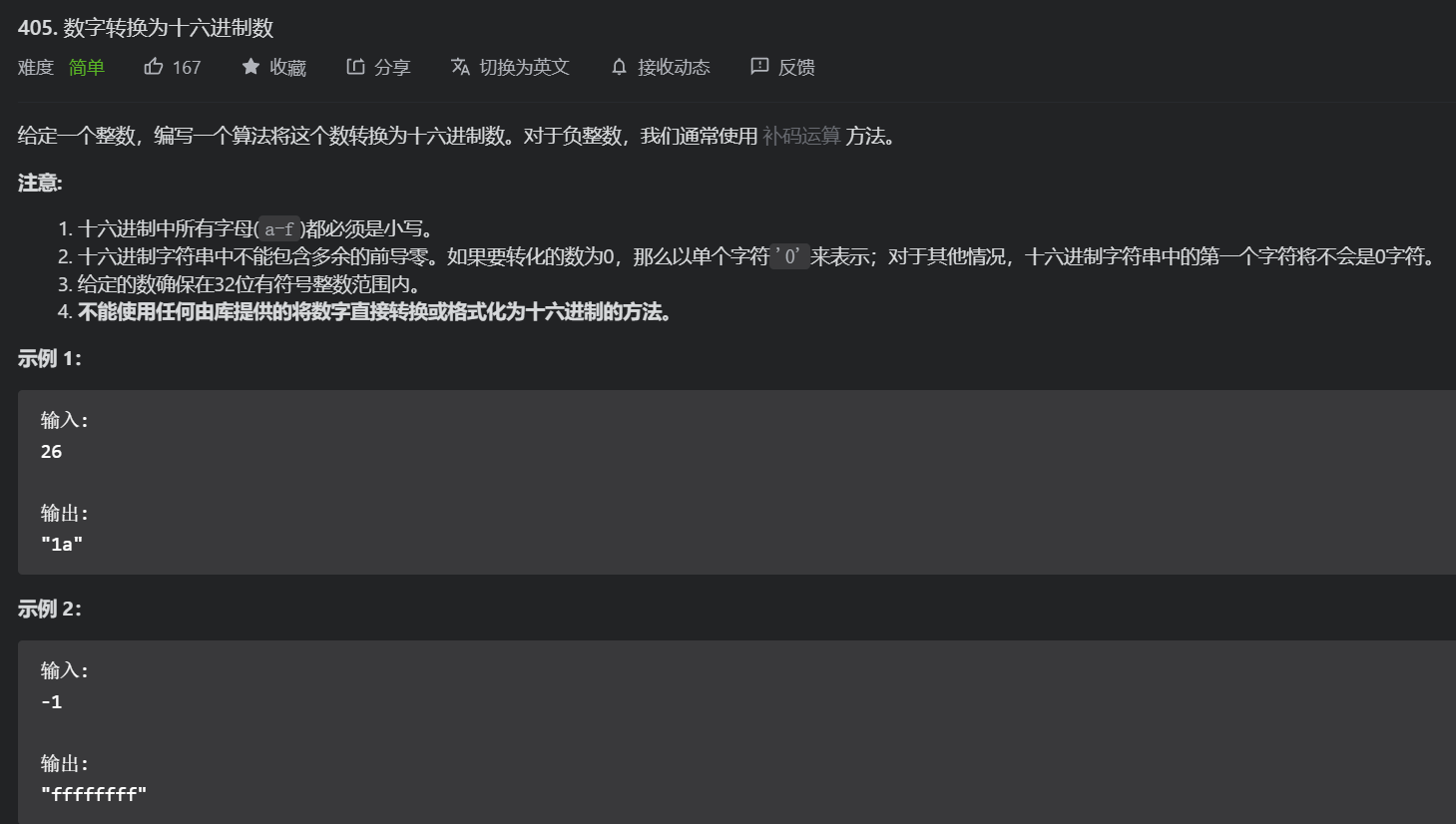
标签:
- 位运算
- 必考
思路:
- 补码运算中,符号位包括 0 和 1。32 位的十六进制数,每四位二进制对应一位十六进制,所以三十二位有符号十六进制数有八位组成。
- 将原数值的二进制数拆分为八组,依次将每组转换为十六进制数即可。
- 第 i 组可以通过
(nums >> (4 * i)) & 0xf得到该组的值,其取值范围是 0 到 15。对于 0 到 9,数字本身就是十六进制数。对于 10 到 15,数字转换为 a 到 f 的字母。 - 对于负整数,第一位肯定不是零,所以肯定不会出现前导零。对于零和正整数,可能出现前导零,因此需要判断。如果数是零,直接返回零。如果不是,则从第一个不是零的值开始拼成十六进制数。
题解:
class Solution {
public String toHex(int num) {
if (num == 0) {
return "0";
}
StringBuffer sb = new StringBuffer();
for (int i = 7; i >= 0; i --) {
int val = (num >> (4 * i)) & 0xf;
if (sb.length() > 0 || val > 0) {
char digit = val < 10 ? (char) ('0' + val) : (char) ('a' + val - 10);
sb.append(digit);
}
}
return sb.toString();
}
}86. 第166题. 分数到小数
参考题解:官方题解
题目:

标签:
- 必考
思路:
题解:
class Solution {
public String fractionToDecimal(int numerator, int denominator) {
long numeratorLong = (long) numerator;
long denominatorLong = (long) denominator;
if (numeratorLong % denominatorLong == 0) {
return String.valueOf(numeratorLong / denominatorLong);
}
StringBuffer sb = new StringBuffer();
if (numeratorLong < 0 ^ denominatorLong < 0) {
sb.append('-');
}
// 整数部分
numeratorLong = Math.abs(numeratorLong);
denominatorLong = Math.abs(denominatorLong);
long integerPart = numeratorLong / denominatorLong;
sb.append(integerPart);
sb.append('.');
// 小数部分
StringBuffer fractionPart = new StringBuffer();
Map<Long, Integer> remainderIndexMap = new HashMap<Long, Integer>();
long remainder = numeratorLong % denominatorLong;
int index = 0;
while (remainder != 0 && !remainderIndexMap.containsKey(remainder)) {
remainderIndexMap.put(remainder, index);
remainder *= 10;
fractionPart.append(remainder / denominatorLong);
remainder %= denominatorLong;
index++;
}
if (remainder != 0) { // 有循环节
int insertIndex = remainderIndexMap.get(remainder);
fractionPart.insert(insertIndex, '(');
fractionPart.append(')');
}
sb.append(fractionPart.toString());
return sb.toString();
}
}87. 第414题. 第三大的数
参考题解:官方题解
题目:
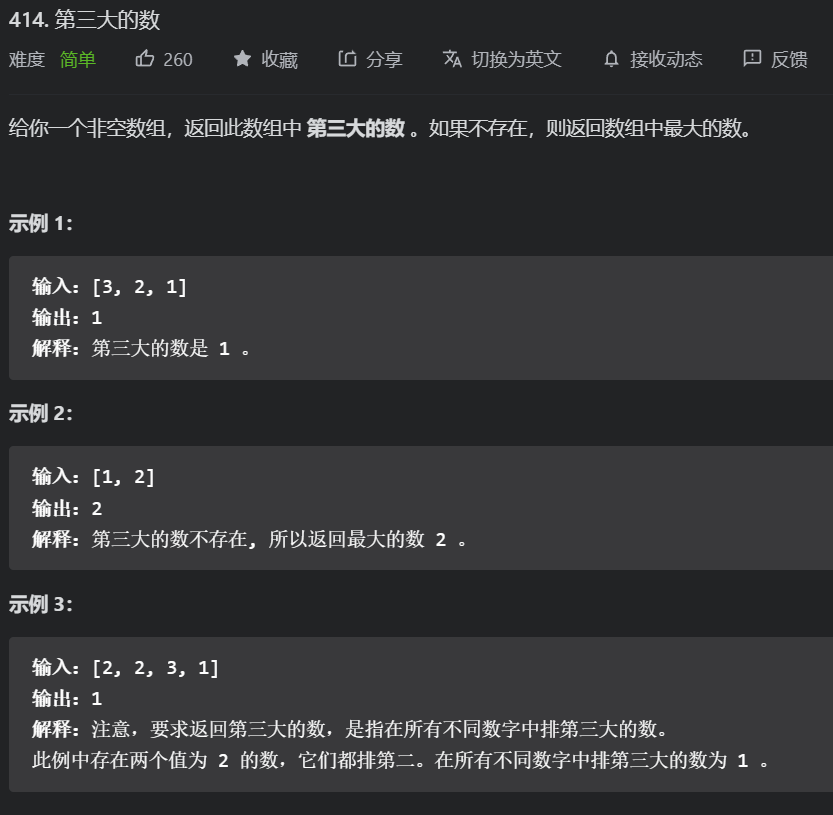
标签:
- 必考。
87.1 去重 + 排序
思路:
- 首先通过 Set 去重,随后用 ArrayList 进行排序。
题解:
class Solution {
public int thirdMax(int[] nums) {
Set<Integer> set = new HashSet<>();
for (int x : nums) set.add(x);
List<Integer> list = new ArrayList<>(set);
Collections.sort(list);
return list.size() < 3 ? list.get(list.size() - 1) : list.get(list.size() - 3);
}
}87.2 有限变量 + 遍历
思路:
- 这种题的最标准方法是设置几个有限变量,然后慢慢求解。
题解:
class Solution {
long INF = (long)-1e18;
public int thirdMax(int[] nums) {
long a = INF, b = INF, c = INF;
for (int x : nums) {
if (x > a) {
c = b; b = a; a = x;
} else if (x < a && x > b) {
c = b; b = x;
} else if (x < b && x > c) {
c = x;
}
}
return c != INF ? (int)c : (int)a;
}
}88. 第352题. 将数据流变为多个不相交区间
参考题解:【宫水三叶】一题双解 :「二分 + 朴素维护区间」&「二分 + 优化维护区间」
题目:
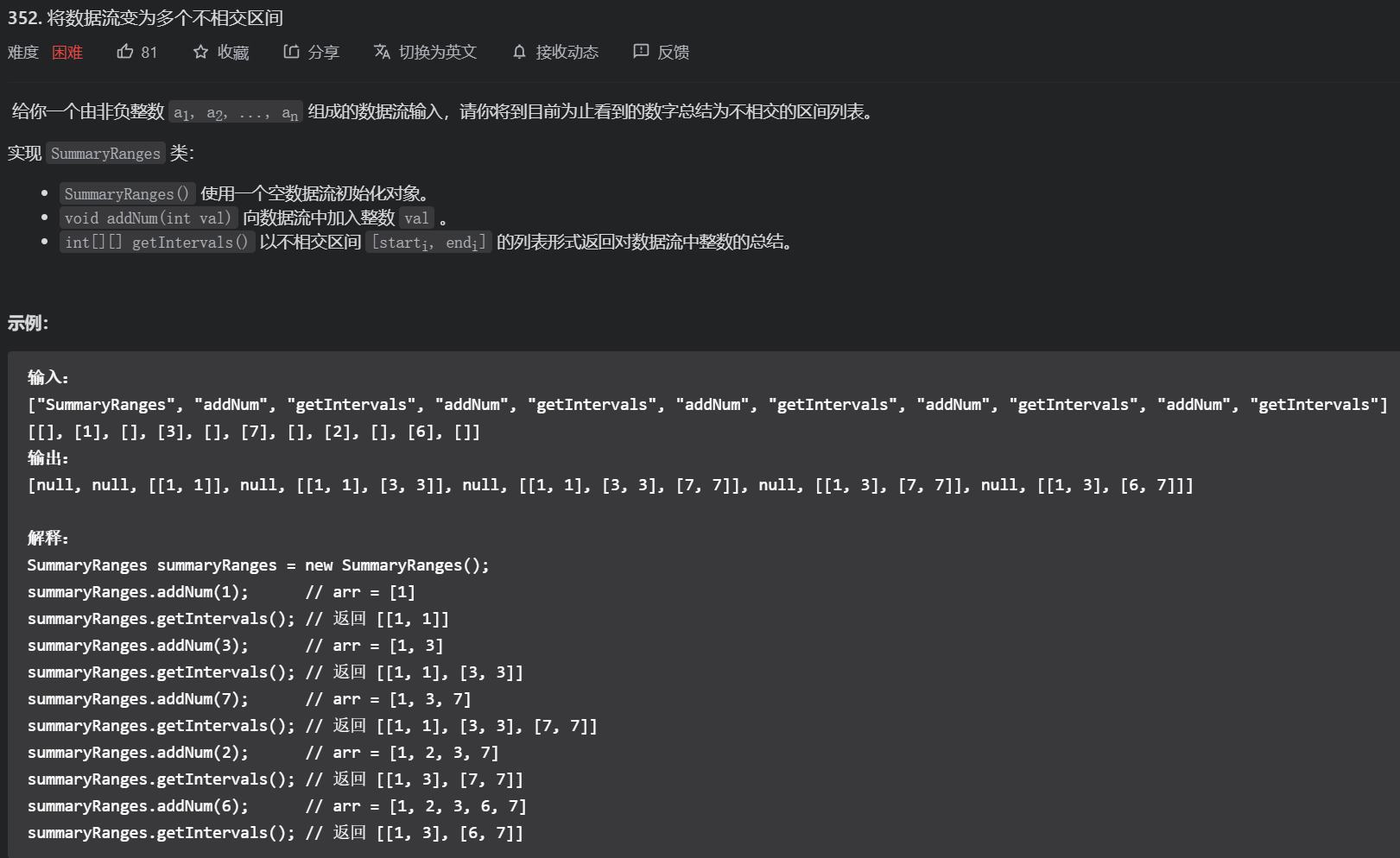
标签:
-
二分查找
-
红黑树
88.1 朴素解法(二分 + 朴素维护区间)
思路:
- 朴素方法就是用 List 维护所有不相交的区间,然后调用 addNum 时先通过二分法找到相邻区间,然后模拟即可。
题解:
class SummaryRanges {
List<int[]> list = new ArrayList<>();
public void addNum(int val) {
int n = list.size();
if (n == 0) {
list.add(new int[]{val, val});
return ;
}
int l = 0, r = n - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (list.get(mid)[0] <= val) l = mid;
else r = mid - 1;
}
int[] cur = list.get(r);
if (cur[0] > val) {
if (val + 1 == cur[0]) {
cur[0] = val;
} else {
list.add(r, new int[]{val, val});
}
return ;
}
if (cur[0] <= val && val <= cur[1]) {
// pass
} else if (r == n - 1) {
if (cur[1] + 1 == val) {
cur[1] = val;
} else {
list.add(new int[]{val, val});
}
} else {
int[] next = list.get(r + 1);
if (cur[1] + 1 == val && val == next[0] - 1) {
cur[1] = next[1];
list.remove(r + 1);
} else if (cur[1] + 1 == val) {
cur[1] = val;
} else if (next[0] - 1 == val) {
next[0] = val;
} else {
list.add(r + 1, new int[]{val, val});
}
}
}
public int[][] getIntervals() {
int n = list.size();
int[][] ans = new int[n][2];
for (int i = 0; i < n; i++) ans[i] = list.get(i);
return ans;
}
}88.2 高级解法(二分 + 优化维护区间)
思路:
- 虽然在 addNum 中使用了复杂度为 O(log m) 的二分查找,但在维护区间时,由于要对 list 进行针对索引的插入和删除,所以整体复杂度为 O(m)。
- 我们期望找到一种插入删除复杂度同样为 O(log m) 的数据结构,这时就可以使用 TreeSet (红黑树)。
- Java 中红黑树 TreeSet 的二分更为简单。可以用 floor 和 ceiling 方法找到当前值的相邻区间。
题解:
class SummaryRanges {
TreeSet<int[]> ts = new TreeSet<>((a, b)->a[0]-b[0]);
int[] head = new int[]{-10, -10}, tail = new int[]{10010, 10010};
public SummaryRanges() {
ts.add(head);
ts.add(tail);
}
public void addNum(int val) {
int[] cur = new int[]{val, val};
int[] prev = ts.floor(cur);
int[] next = ts.ceiling(cur);
if ((prev[0] <= val && val <= prev[1]) || (next[0] <= val && val <= next[1])) {
// pass
} else if (prev[1] + 1 == val && next[0] - 1 == val) {
prev[1] = next[1];
ts.remove(next);
} else if (prev[1] + 1 == val) {
prev[1] = val;
} else if (next[0] - 1 == val) {
next[0] = val;
} else {
ts.add(cur);
}
}
public int[][] getIntervals() {
// using ceiling
// int n = ts.size();
// int[][] ans = new int[n - 2][2];
// int[] cur = head;
// for (int i = 0; i < n - 2; i++) {
// ans[i] = ts.ceiling(new int[]{cur[0] + 1, cur[1] + 1});
// cur = ans[i];
// }
// return ans;
// using iterator
int n = ts.size();
int[][] ans = new int[n - 2][2];
Iterator<int[]> iterator = ts.iterator();
iterator.next();
for (int i = 0; i < n - 2; i++) ans[i] = iterator.next();
return ans;
}
}89. 第5题. 最长回文子串
个人题解:动态规划求解最长回文串问题
题目:
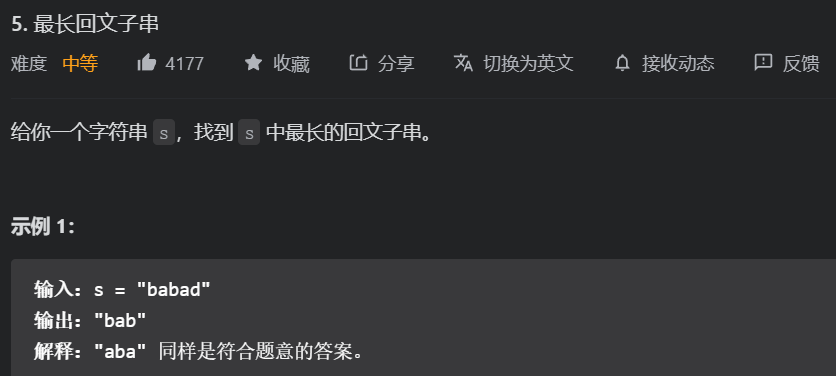
标签:
- 动态规划
- 必考
思路:
- 最长回文串是一种典型的动态规划问题,而且相对于最长匹配子串之类的问题,更有难度。
- 不过,和一般的动态规划问题不同的是,最长回文串的
dp是用于保存左右区间内的串是否是回文串的,而不是保存最长长度的。 - 所以,对问题需要进行两层遍历。外层是回文串长度,内层是左侧区间。
- 初始状态是
dp[i][i] = true。此外还有if (length == 2 && c[left] == c[right]) dp[left][right] = true。 - 状态转移是从长度较短的向长度较长的转移
if (length > 2 && c[left] == c[right]) dp[left][right] = dp[left + 1][right - 1]。 - 此外,返回的内容是字符串,由于记录最长长度是必要的,因此我们可以再记录一个
begin,最后返回s.substring(begin, begin + max_length)即可!
题解:
class Solution {
public String longestPalindrome(String s) {
char[] charArray = s.toCharArray();
int n = s.length(), max_length = 1, begin = 0;
boolean[][] dp = new boolean[n][n];
for (int i = 0; i < n; ++i) {
dp[i][i] = true;
}
for (int length = 2; length <= n; ++length) {
for (int left = 0; left < n; ++left) {
int right = left + length - 1;
if (right >= n) {
break;
}
if (charArray[left] != charArray[right]) {
dp[left][right] = false;
} else if (length == 2) {
dp[left][right] = true;
} else {
dp[left][right] = dp[left + 1][right - 1];
}
if (dp[left][right] == true && length > max_length) {
max_length = length;
begin = left;
}
}
}
return s.substring(begin, begin + max_length);
}
}90. 第3题. 无重复字符的最常子串
个人题解:滑动窗口求解无重复字符的最长子串
题目:
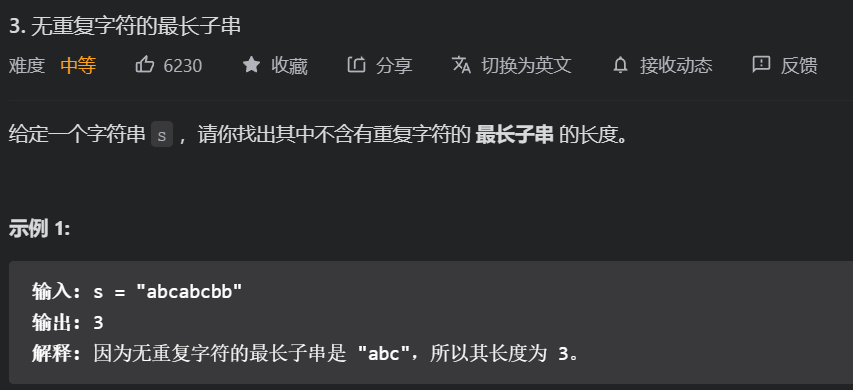
标签:
- 必考
- 滑动窗口
思路:
- 这道题的关键就在于,选择滑动窗口方法。
- 窗口内的内容,为了快速判断有没有重复字符,我们直接构造一个 HashSet。
- 之后,每次遇到值都判断是否有重复值,如果有就滑动窗口。没有的话就添加进来然后判断长度。
题解:
class Solution {
public int lengthOfLongestSubstring(String s) {
if (s.length() == 0) {
return 0;
}
char[] c = s.toCharArray();
HashSet<Character> set = new HashSet<>();
int n = c.length, res = 1, val = 0;
for (int i = 0; i < n; ++i) {
while (set.contains(c[i])) {
set.remove(c[val++]);
}
set.add(c[i]);
if (set.size() > res) {
res = set.size();
}
}
return res;
}
}91. 第273题. 整数转换英文表示
参考题解:
题目:
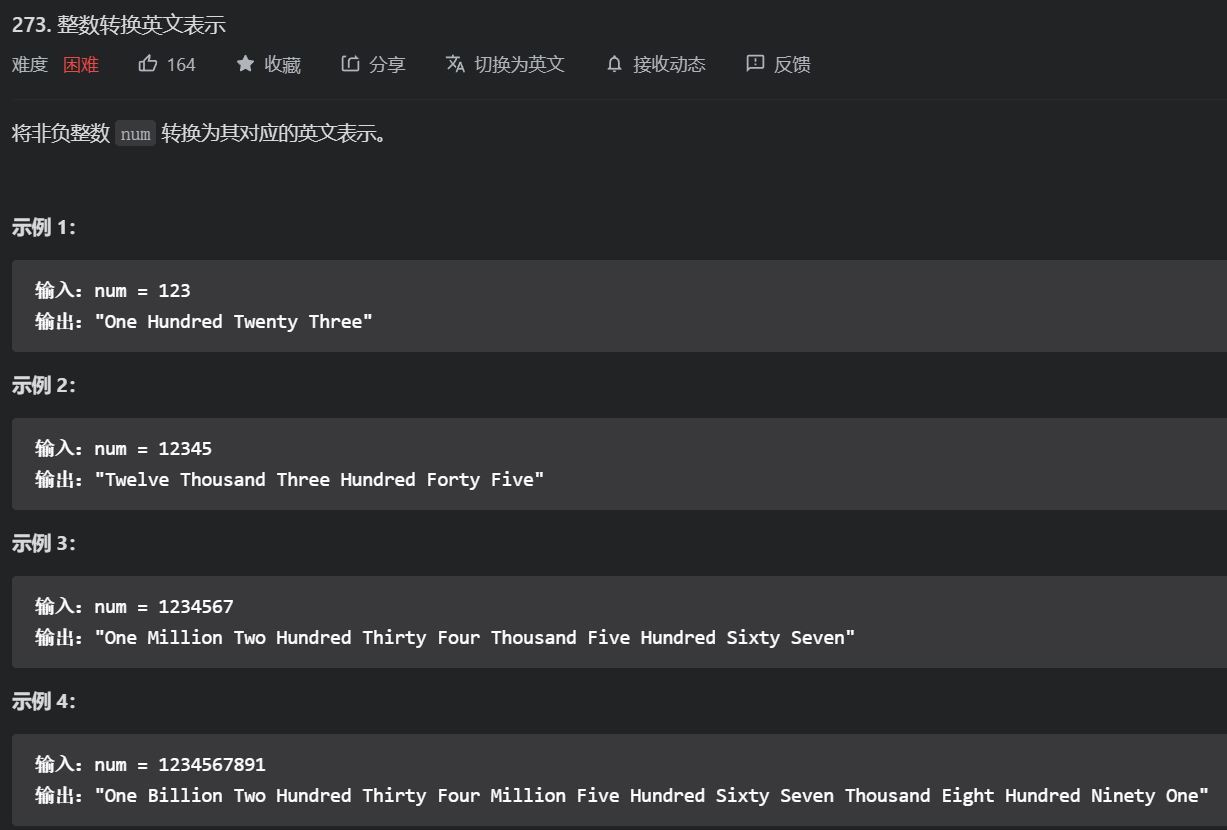
标签:
- 恶心
思路:
- 2^31 内最多是10位数,这个范围内英文需要有 4 种标签:个位、十位、二十位和千位。
- 首先判断零。英文表示里除了 0 以外,中间是不会出现 zero 的。
- 随后 unit 设置为 10^9。i 设置为 3。每次 i--,unit /= 1000。
- 调用函数更新其中内容。
- 这道题非常不好写。最好多看看,背下来。
题解:
class Solution {
String[] singles = {"", "One", "Two", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine"};
String[] teens = {"Ten", "Eleven", "Twelve", "Thirteen", "Fourteen", "Fifteen", "Sixteen", "Seventeen", "Eighteen", "Nineteen"};
String[] tens = {"", "Ten", "Twenty", "Thirty", "Forty", "Fifty", "Sixty", "Seventy", "Eighty", "Ninety"};
String[] thousands = {"", "Thousand", "Million", "Billion"};
public String numberToWords(int num) {
if (num == 0) {
return "Zero";
}
StringBuffer sb = new StringBuffer();
for (int i = 3, unit = 1000000000; i >= 0; i--, unit /= 1000) {
int curNum = num / unit;
if (curNum != 0) {
num -= curNum * unit;
StringBuffer curr = new StringBuffer();
recursion(curr, curNum);
curr.append(thousands[i]).append(" ");
sb.append(curr);
}
}
return sb.toString().trim();
}
public void recursion(StringBuffer curr, int num) {
if (num == 0) {
return;
} else if (num < 10) {
curr.append(singles[num]).append(" ");
} else if (num < 20) {
curr.append(teens[num - 10]).append(" ");
} else if (num < 100) {
curr.append(tens[num / 10]).append(" ");
recursion(curr, num % 10);
} else {
curr.append(singles[num / 100]).append(" Hundred ");
recursion(curr, num % 100);
}
}
}92. 第7题. 整数反转
参考题解:评论区dalao
题目:
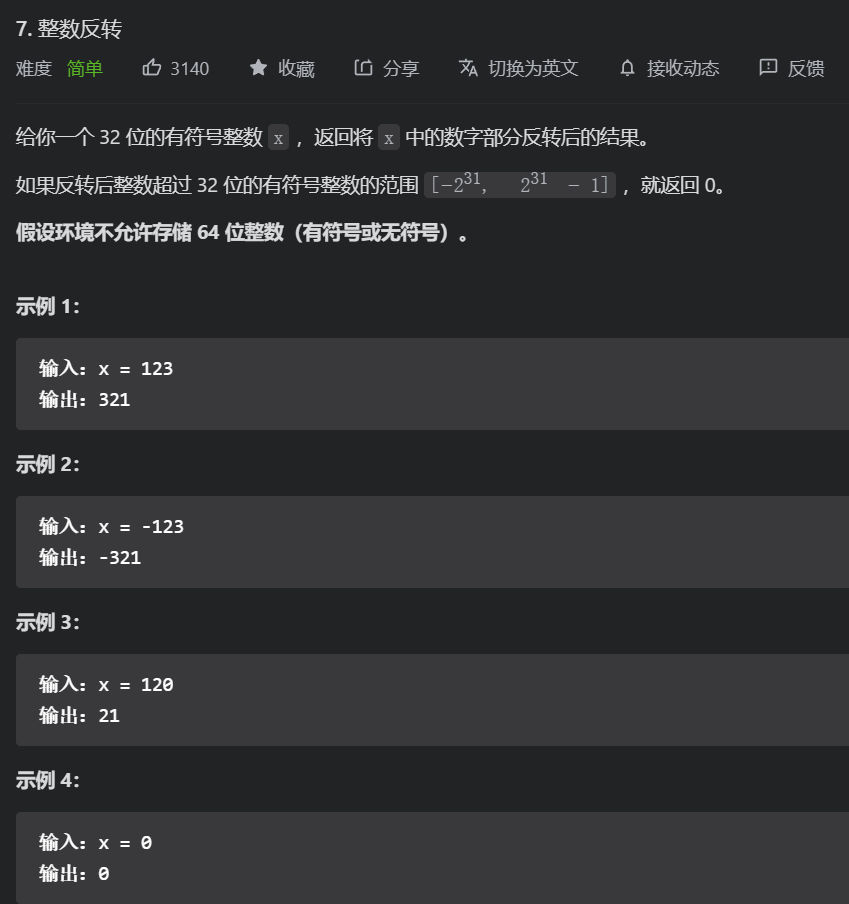
标签:
- 恶心。
- 意想不到。
思路:
- 首先,这道题是反转整数,但是反转结果有可能大于 32 位整数的极限,因此如果超过要返回 0。
- 那么,如何简洁明了的完成这道题呢?可以用 long 记录反转的数,最后用
(int)n == n ? (int)n : 0;结束即可。
题解:
class Solution {
public int reverse(int x) {
long n = 0;
while(x != 0) {
n = n * 10 + x % 10;
x = x / 10;
}
return (int)n == n ? (int)n : 0;
}
}93. 第476题. 数字的补数
参考题解:【宫水三叶】一题双解 :「遍历」&「lowbit」
题目:
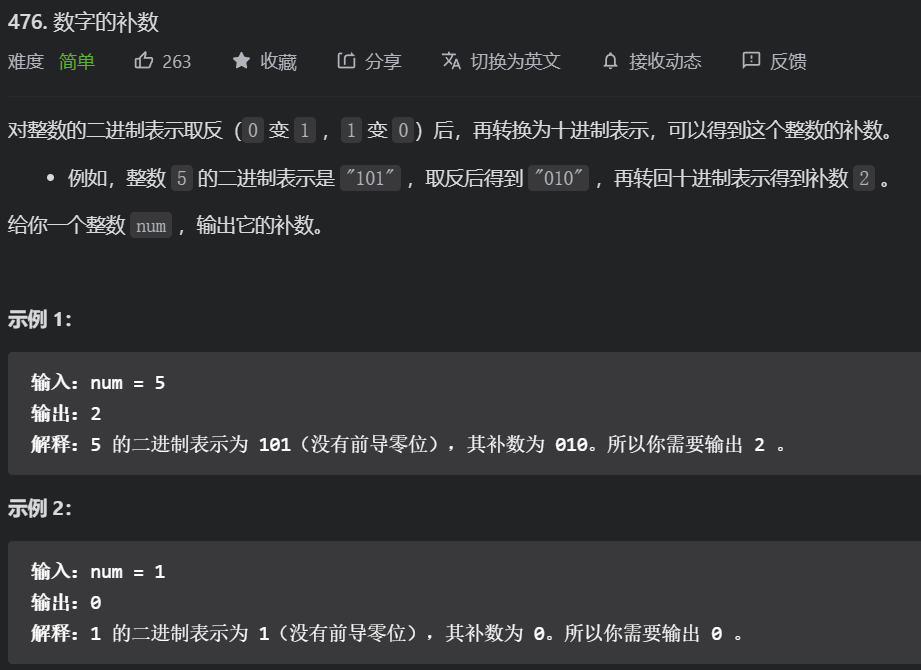
标签:
- 位运算
- 必考
思路:
- 这道题的按位取反,同时用到了 &、^、<<、>>、|= 五种运算符,可以说是集大成者。
- ans 每次要 |= 取反位,这样才能每次更新一位的值。
- num & 1 ^ 1 是每次取最低位进行取逆。
- ans 每次都要 << i++,同时 num >>= 1。
题解:
class Solution {
public int findComplement(int num) {
int ans = 0, i = 0;
while (num != 0) {
//按位取反
ans |= ((num & 1 ^ 1) << i++);
num >>= 1;
}
return ans;
}
}94. 第74题. 搜索二维矩阵
个人题解:两次二分查找求解问题,双100%
题目:

标签:
- 二分查找
思路:
- 就是两遍二分查找。
- 二分查找需要注意的点:
- right 要取 length - 1;
mid = left + ((right - left) >> 1);
left = mid + 1, right = mid - 1。
题解:
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int m = matrix.length, n = matrix[0].length;
int left = 0, right = m - 1;
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (matrix[mid][0] <= target && matrix[mid][n - 1] >= target) {
int newLeft = 0, newRight = n - 1;
while (newLeft <= newRight) {
int newMid = newLeft + ((newRight - newLeft) >> 1);
if (matrix[mid][newMid] == target) {
return true;
} else if (matrix[mid][newMid] < target) {
newLeft = newMid + 1;
} else {
newRight = newMid - 1;
}
}
return false;
} else if (matrix[mid][0] > target) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return false;
}
}95. 第869题. 重新排序得到2的幂
参考题解:官方题解
题目:

标签:
- 必考
- 哈希
- 位操作
思路:
- 这道题是非常好的一道题!!建议经常回顾。
- 科学计数法:1e9。
- 字符数组转字符串可以直接用 new String(charArray)。
- 2 的幂可以用 i <<= 1 来逐步获得。
题解:
class Solution {
Set<String> set = new HashSet<>();
public void init() {
for (int i = 1; i <= 1e9; i <<= 1) {
set.add(countDigits(i));
}
}
public String countDigits(int n) {
char[] cnt = new char[10];
while (n > 0) {
++cnt[n % 10];
n /= 10;
}
return new String(cnt);
}
public boolean reorderedPowerOf2(int n) {
init();
return set.contains(countDigits(n));
}
}96. 第260题. 只出现一次的数字3
参考题解:官方题解
题目:
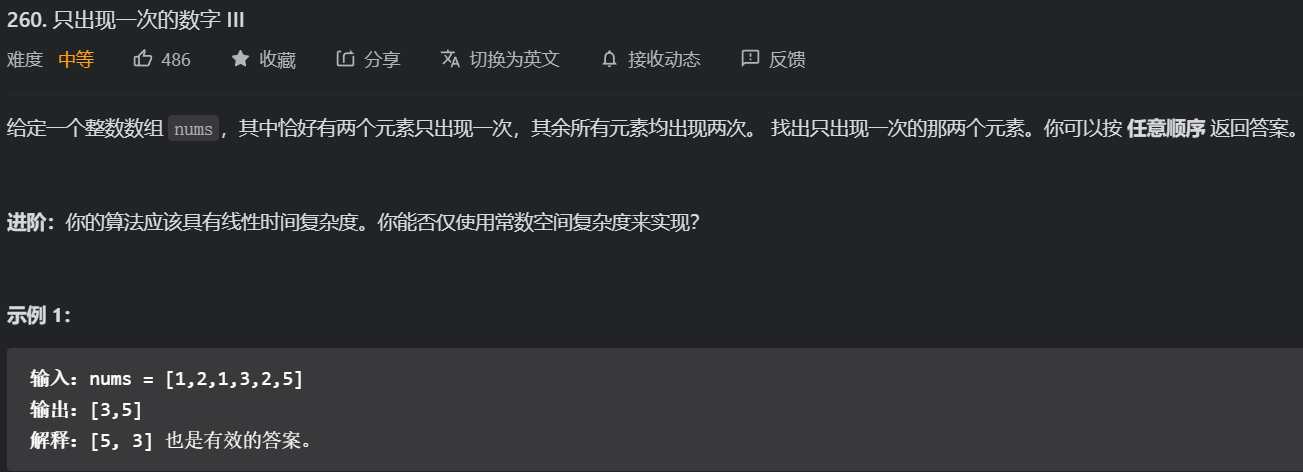
标签:
- 位运算
- 恶心
思路:
- 这道题很容易想到用位运算,但是其实很难写!!
- 首先用异或扫一遍,然后需要用 temp & (-temp) 进行调整,之后再用 & i 是否为 0 判断是两个数字中的哪一个的元素,然后用 ^= 再累加位数,最后才能得到答案。
- 背下来这个过程就好。
题解:
class Solution {
public int[] singleNumber(int[] nums) {
int temp = 0, val = 0;;
int[] res = new int[2];
for (int i : nums) {
temp ^= i;
}
temp = (temp == Integer.MIN_VALUE ? temp : temp & (-temp));
for (int i : nums) {
if ((temp & i) != 0) {
res[0] ^= i;
} else {
res[1] ^= i;
}
}
return res;
}
}97. 第268题. 丢失的数字
参考题解:官方题解
题目:
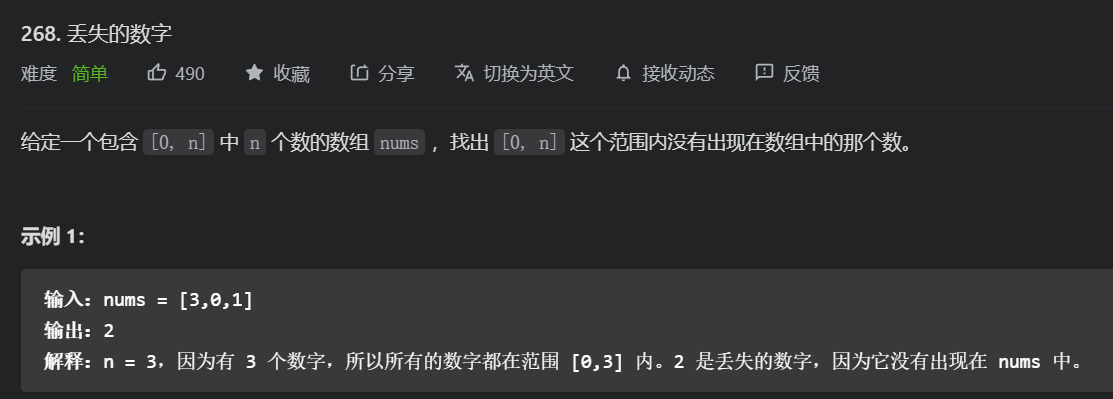
标签:
- 必考
- 位运算
思路:
- 可以对 0 到 n 和 原来的数字,全部进行异或运算,最后结果就是缺失的数字。
- 原理是
0 ^ x = x, x ^ x = 0。
题解:
class Solution {
public int missingNumber(int[] nums) {
int res = 0;
for (int i = 0; i < nums.length; ++i) {
res ^= nums[i];
}
for (int i = 0; i <= nums.length; ++i) {
res ^= i;
}
return res;
}
}98. 第35题. 搜索插入位置
参考题解:[官方题解]()
题目:
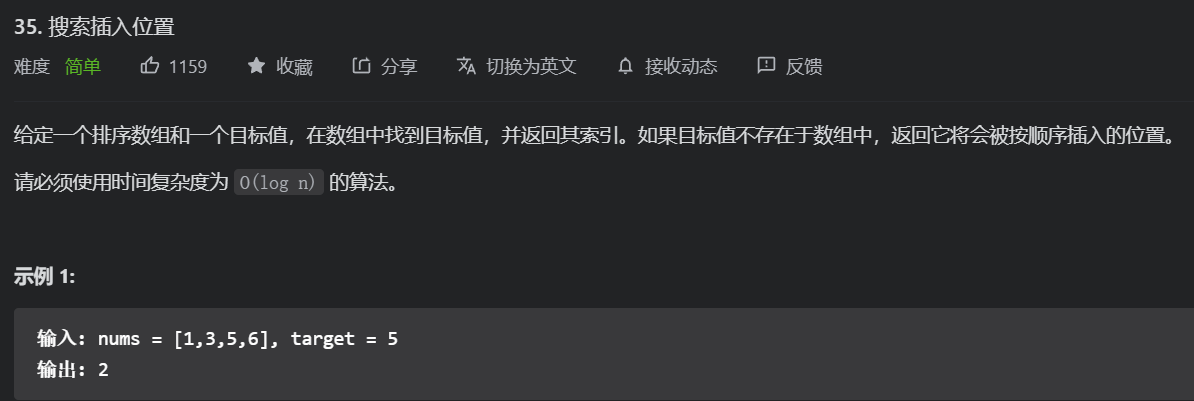
标签:
- 必考
- 模板
- 二分查找
思路:
- 依旧是二分查找题。但是这道题要求将找不到的数字返回插入位置。
- 所以当
nums[mid] < target时,要将left = mid + 1,这样才能确保最后插入位置的正确。
题解:
class Solution {
public int searchInsert(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] >= target) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return left;
}
}99. 第299题. 猜数字游戏
个人题解:HashMap 求解问题
题目:
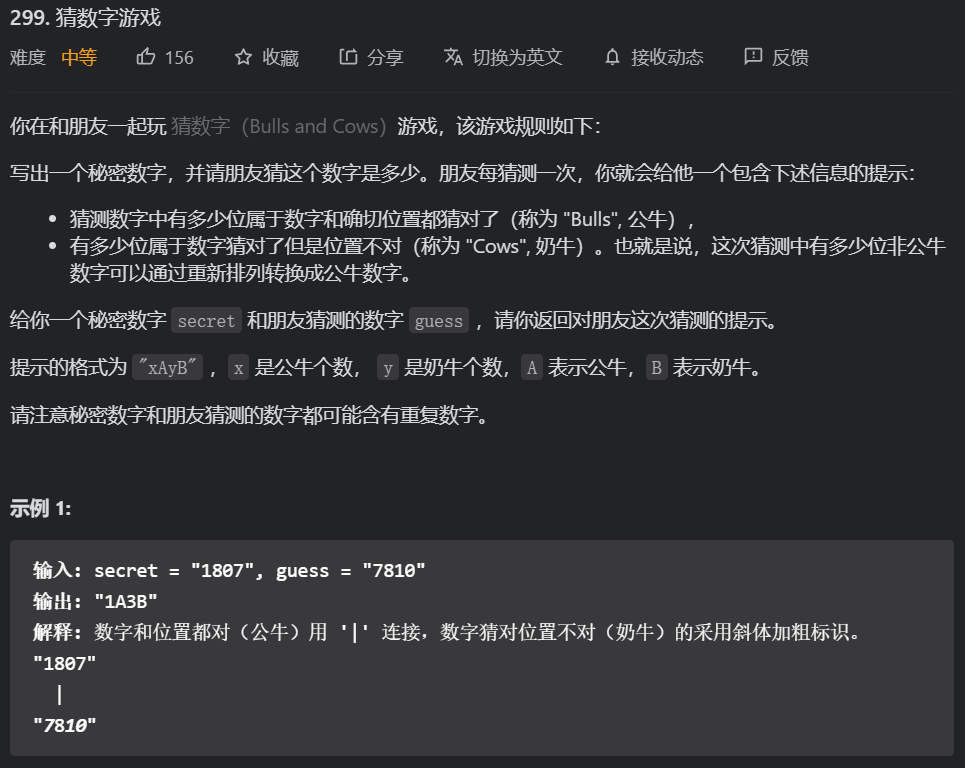
标签:
- 哈希表
- 必考
思路:
- 这道题用哈希表求解就行。但是一定要注意,先比较对位的,再比较不对位的,不然会出错。
题解:
class Solution {
public String getHint(String secret, String guess) {
char[] c1 = secret.toCharArray(), c2 = guess.toCharArray();
HashMap<Character, Integer> map = new HashMap<>();
StringBuffer sb = new StringBuffer();
int a1 = 0, a2 = 0;
for (int i = 0; i < c2.length; ++i) {
if (c1[i] == c2[i]) {
++a1;
} else {
map.put(c2[i], map.getOrDefault(c2[i], 0) + 1);
}
}
for (int i = 0; i < c2.length; ++i) {
if (c1[i] != c2[i] && map.getOrDefault(c1[i], 0) > 0) {
++a2;
map.put(c1[i], map.get(c1[i]) - 1);
}
}
sb.append(a1 + "A" + a2 + "B");
return sb.toString();
}
}100. 第318题. 最大单次长度乘积
个人题解:利用位运算快速求解问题
题目:
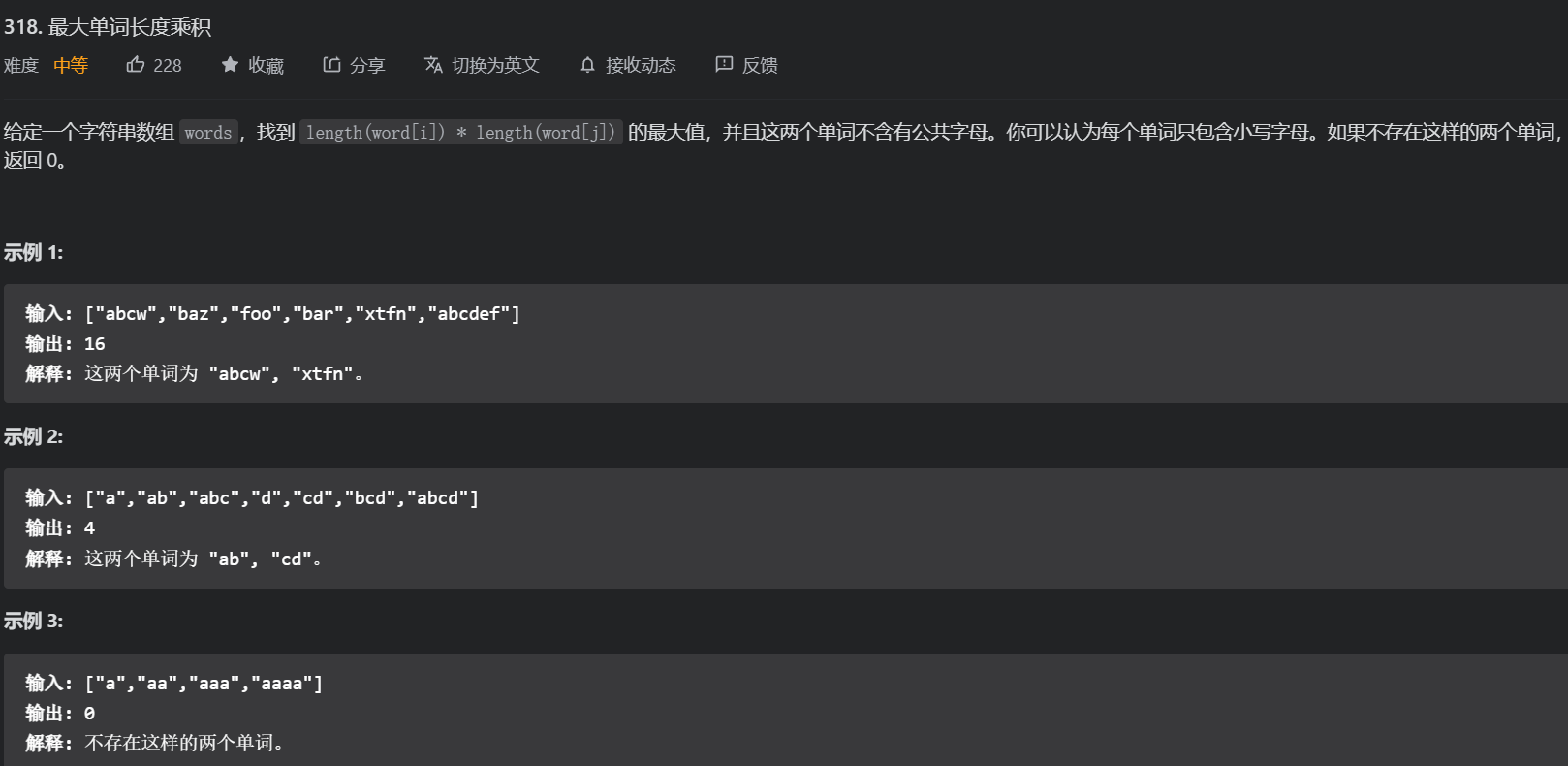
标签:
- 必考
- 位运算
思路:
- 位运算可以用于表示每个单词。
- 随后用位运算就可以比较单次是否有公共字母。
题解:
class Solution {
public int maxProduct(String[] words) {
int[] nums = new int[words.length];
int res = 0;
for (int i = 0; i < words.length; ++i) {
int n = words[i].length();
for (int j = 0; j < n; ++j) {
nums[i] |= (1 << (words[i].charAt(j) - 'a'));
}
// System.out.println(Integer.toBinaryString(nums[i]));
}
for (int i = 0; i < words.length; ++i) {
for (int j = 0; j < words.length; ++j) {
if (i == j) {
continue;
}
if ((nums[i] & nums[j]) == 0) {
res = Math.max(res, words[i].length() * words[j].length());
}
}
}
return res;
}
}101. 第397题. 整数替换
参考题解:官方题解
题目:
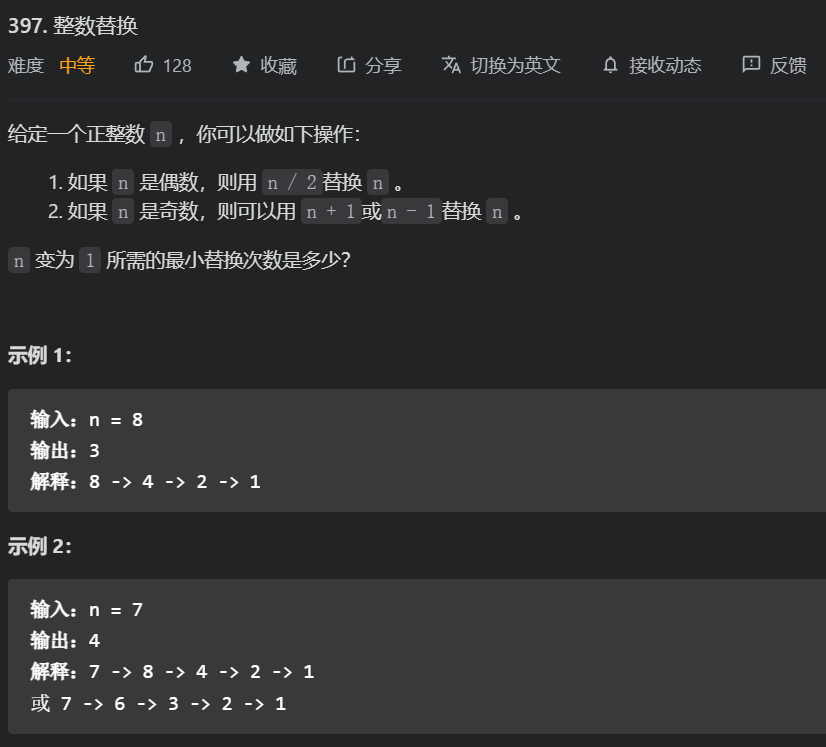
标签:
- 必考
- 记忆化搜索
- 贪心法
101.1 暴力法
思路:
- 用递归方法获取所有 n 到 1 的序列。
- 当 n 为偶数时,只有一种变换方法,n / 2。
- 当 n 为奇数时,加一或减一都会使 n 变为偶数,所以下一步是除以 2,可以将这步转换为两步。(n + 1) / 2 和 (n - 1) / 2。
- 为了避免溢出,可以将 (n + 1) / 2 转换为向下取整的 n / 2 + 1,将 (n - 1) / 2 转换为向下取整的 n / 2。
题解:
class Solution {
public int integerReplacement(int n) {
if (n == 1) {
return 0;
}
if (n % 2 == 0) {
return 1 + integerReplacement(n / 2);
}
return 2 + Math.min(integerReplacement(n / 2), integerReplacement(n / 2 + 1));
}
}101.2 记忆化搜索
思路:
- 可以在外层用 HashMap 保存所有中间结果,从而降低时间复杂度。
题解:
class Solution {
private HashMap<Integer, Integer> map = new HashMap<>();
public int integerReplacement(int n) {
if (n == 1) {
return 0;
}
if (!map.containsKey(n)) {
if (n % 2 == 0) {
map.put(n, 1 + integerReplacement(n / 2));
} else {
map.put(n, 2 + Math.min(integerReplacement(n / 2 + 1), integerReplacement(n / 2)));
}
}
return map.get(n);
}
}101.3 贪心法
思路:
- 比较复杂。

题解:
class Solution {
public int integerReplacement(int n) {
int ans = 0;
while (n != 1) {
if (n % 2 == 0) {
++ans;
n /= 2;
} else if (n % 4 == 1) {
ans += 2;
n /= 2;
} else {
if (n == 3) {
ans += 2;
n = 1;
} else {
ans += 2;
n = n / 2 + 1;
}
}
}
return ans;
}
}102. 第384题. 打乱数组
个人题解:调用 Collection.shuffle 函数解决问题
题目:
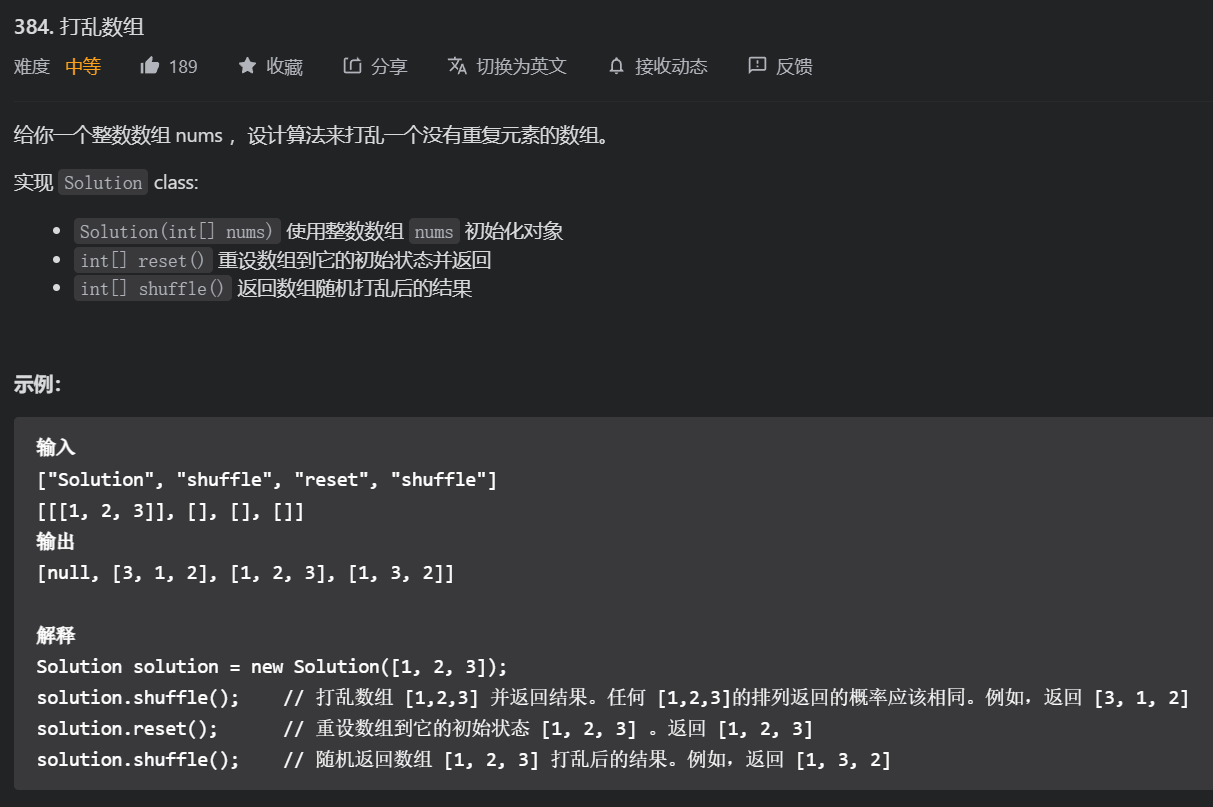
标签:
- 编程能力提升
思路:
- 这道题思路比较简单,但是写的时候有一些比较有趣的地方。
- Array 数组复制:
int[] intA = (int[]) Arrays.copyOf(intB, intB.length); - int array 转 Integer list:
List<Integer> listA = Arrays.stream(intA).boxed().collect(Collectors.toList()); - Integer list 转 int array:
int[] intB = listB.stream().mapToInt(Integer::intValue).toArray(); - 重排序:
Collections.shuffle(listA);
题解:
class Solution {
private int[] val;
private List<Integer> list;
public Solution(int[] nums) {
this.val = (int[]) Arrays.copyOf(nums, nums.length);
this.list = Arrays.stream(this.val).boxed().collect(Collectors.toList());
}
public int[] reset() {
return this.val;
}
public int[] shuffle() {
Collections.shuffle(this.list);
int[] res = this.list.stream().mapToInt(Integer::intValue).toArray();
return res;
}
}103. 第1034题. 边界着色
个人题解:深度优先遍历求解问题
题目:
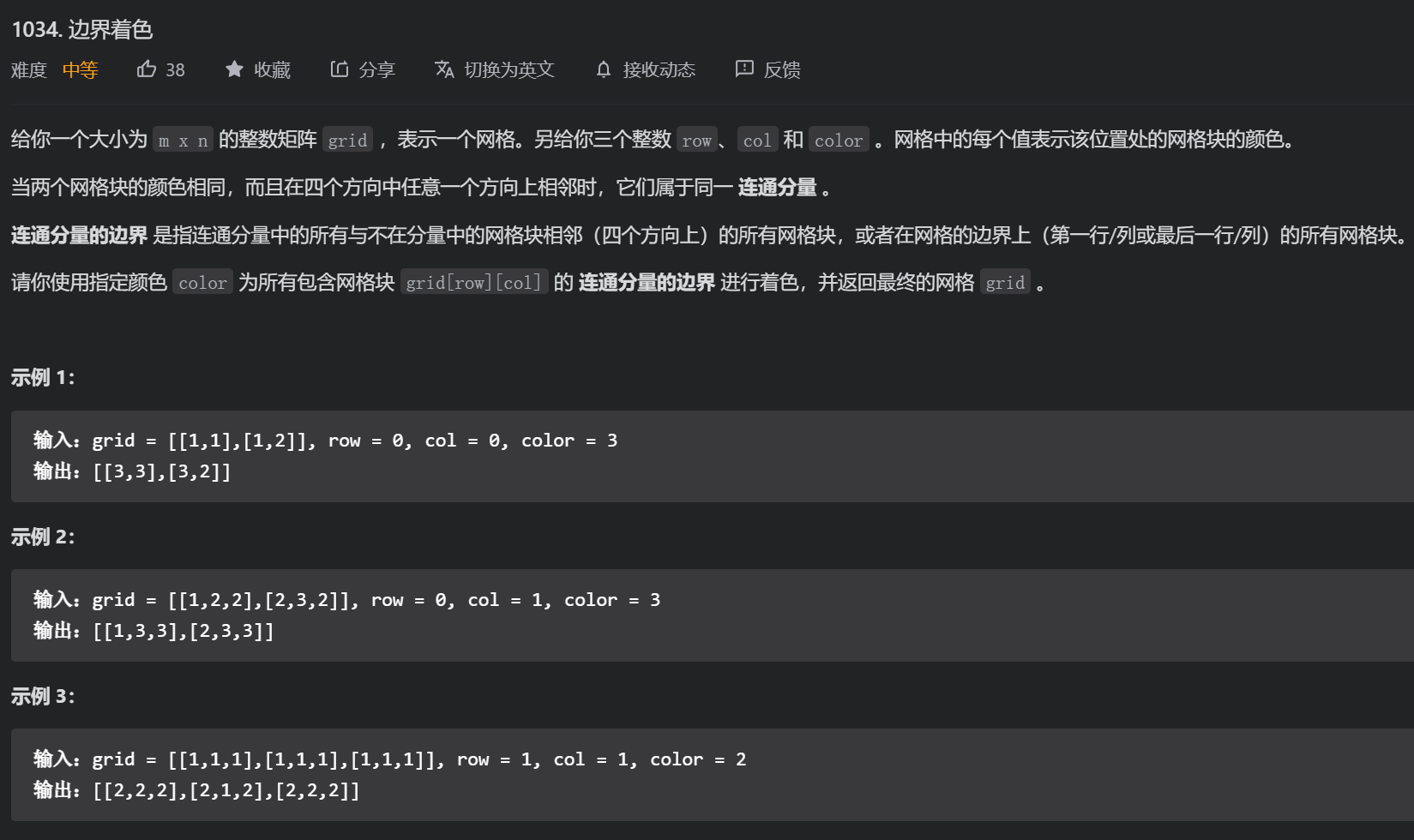
标签:
- 必考
- 深度优先遍历
思路:
- 深度优先遍历求解问题。
- 但是要注意边界条件判断。同时需要有一个 visit 列表。
题解:
class Solution {
private int[][] grid;
private boolean[][] visit;
private int l1;
private int l2;
private int oldColor;
private List<int[]> border;
public int[][] colorBorder(int[][] grid, int row, int col, int color) {
this.grid = grid;
this.l1 = grid.length;
this.l2 = grid[0].length;
this.oldColor = grid[row][col];
this.border = new ArrayList<>();
this.visit = new boolean[l1][l2];
visit[row][col] = true;
dfs(row, col, color);
Iterator<int[]> it = border.iterator();
while (it.hasNext()) {
int[] temp = it.next();
grid[temp[0]][temp[1]] = color;
}
return grid;
}
private void dfs(int row, int col, int color) {
boolean isBorder = false;
int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
for (int i = 0; i < dir.length; ++i) {
int r = row + dir[i][0], c = col + dir[i][1];
if (r > l1 - 1 || r < 0 || c > l2 - 1 || c < 0 || grid[r][c] != oldColor) {
isBorder = true;
} else if (!visit[r][c]) {
visit[r][c] = true;
dfs(r, c, color);
}
}
if (isBorder) {
border.add(new int[]{row, col});
}
}
}104. 第911题. 在线选举
个人题解:二分查找找到满足要求的最大下标
题目:
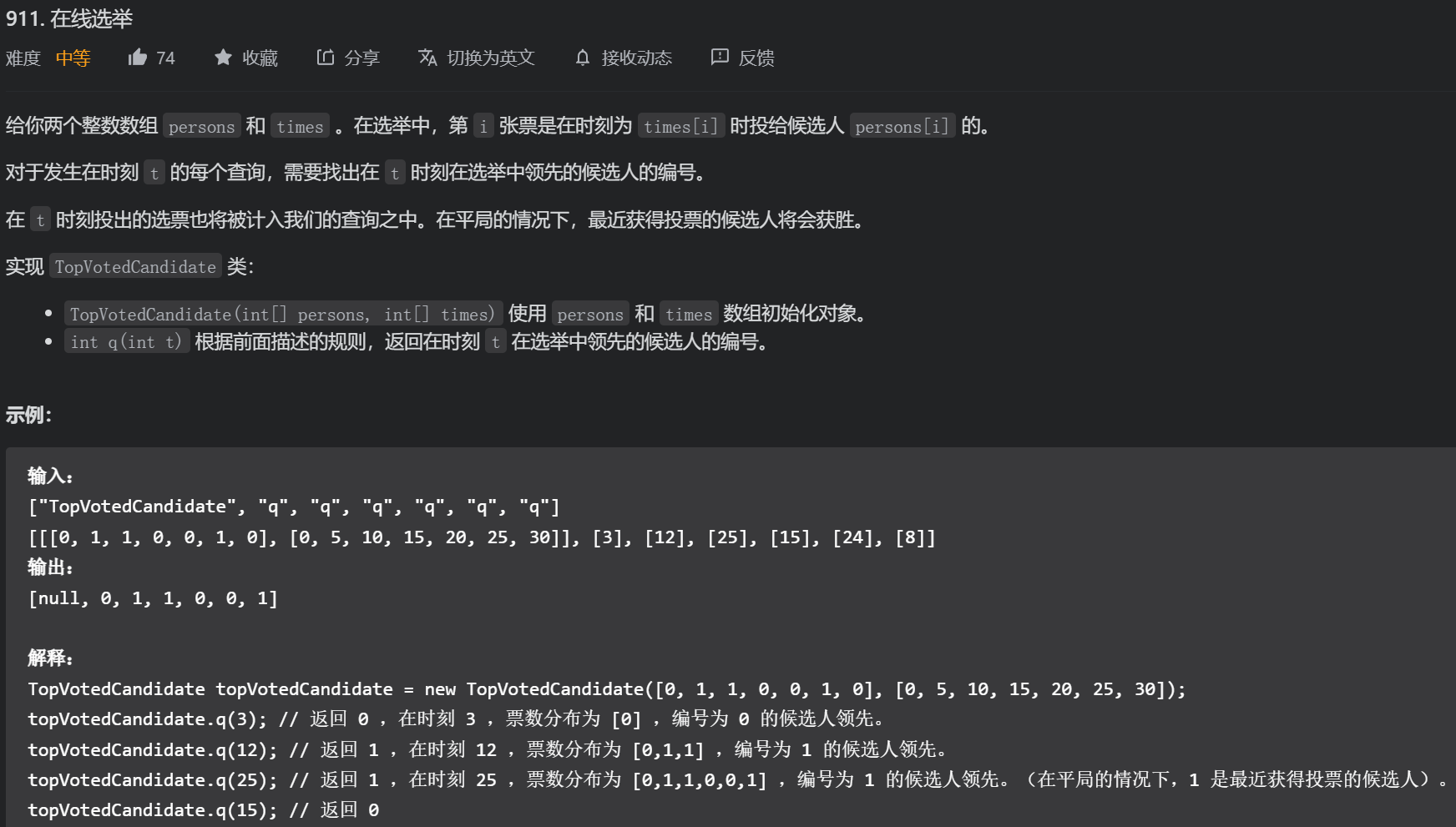
标签:
- 必考
- 二分查找(右边界)
思路:
- 这道题一眼就能看出来是二分查找。不过,重点是:这个是右侧边界的二分查找!
- 右侧边界的二分查找,注意 int mid = left + ((right - left) >> 1) + 1;!
- 同时,右侧边界二分查找,要变 right = mid - 1; 和 left = mid;,这个不要记错了!
- 最后,结果是 res[right]!
题解:
class TopVotedCandidate {
private HashMap<Integer, Integer> map;
int[] times;
int[] res;
public TopVotedCandidate(int[] persons, int[] times) {
this.map = new HashMap<>();
int n = persons.length, max = 0, maxId = 0;
this.res = new int[n];
this.times = times;
for (int i = 0; i < n; ++i) {
map.put(persons[i], map.getOrDefault(persons[i], 0) + 1);
int temp = map.get(persons[i]);
if (temp >= max) {
max = temp;
maxId = persons[i];
}
res[i] = maxId;
}
}
public int q(int t) {
int left = 0, right = res.length - 1;
while (left < right) {
int mid = left + ((right - left) >> 1) + 1;
if (times[mid] > t) {
right = mid - 1;
} else {
left = mid;
}
}
return res[right];
}
}105. 第630题. 课程表3
参考题解:官方题解
题目:
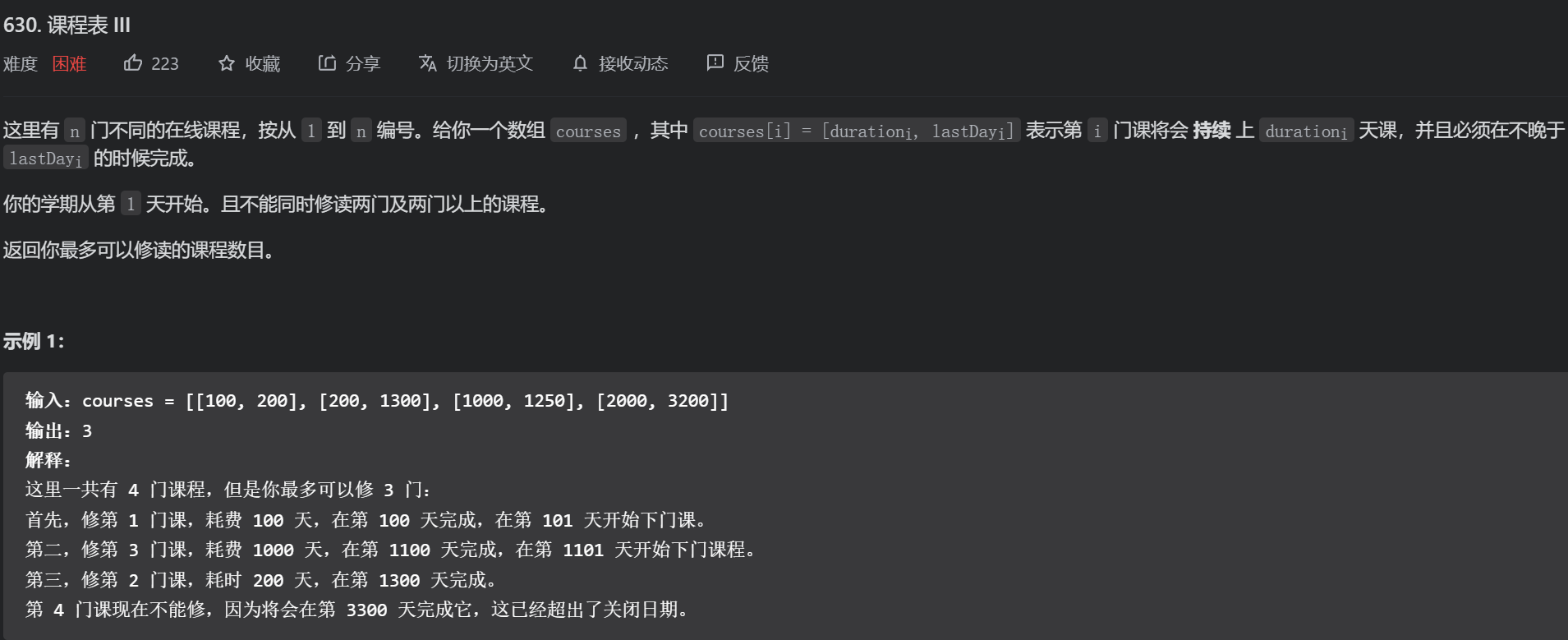
标签:
- 优先队列
- 贪心
思路:
- 这道题是典型的贪心法。
- 首先按照结束的时间排序。
- 其次,构建已经选择课程的队列,给其第一个参数提供一个排序 lambda 表达式,表示按照持续时间排序,而且要反向排序,时间长的放在前面。
- 随后,遍历课程,判断是否有更短的课程,优先选择更短的课程,将其放到队列中。
题解:
class Solution {
public int scheduleCourse(int[][] courses) {
// 以结束时间排序
Arrays.sort(courses, (c1, c2) -> c1[1] - c2[1]);
// 储存已选择的课程,按照持续时间排序
PriorityQueue<int[]> heap = new PriorityQueue<>((c1, c2) -> c2[0] - c1[0]);
int day = 0;
for (int[] c : courses) {
if (day + c[0] <= c[1]) {
// 如果当前课程时间不冲突,将该课程加入队列
// 这里的不冲突可以理解为,0~day+c[0]这段区间,我们还可以再插入当前一节课
day += c[0];
heap.offer(c);
} else if (!heap.isEmpty() && heap.peek()[0] > c[0]) {
// 课程时间冲突,且有选过其他课,这时我们找到最长时间的课程,用当前的短课替换了,余出了更多的空区间
// 所以这里我们余出的时间其实就是两者的持续时间之差,课程变短了,day会前移,这样我们相当于变相给后面的课程增加了选择的区间
day -= heap.poll()[0] - c[0];
heap.offer(c);
}
}
return heap.size();
}
}106. 第48题. 旋转图像
参考题解:官方题解
题目:

标签:
- 必考
- 思维题
思路:
-
旋转 90 度,只需要考虑 1/4 的矩形面积。
-
每个部分按照以下方法,旋转。
-
int temp = matrix[x][y]; matrix[x][y] = matrix[n - y - 1][x]; matrix[n - y - 1][x] = matrix[n - x - 1][n - y - 1]; matrix[n - x - 1][n - y - 1] = matrix[y][n - x - 1]; matrix[y][n - x - 1] = temp;
题解:
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
int limit1 = n / 2, limit2 = (n + 1) / 2;
for (int x = 0; x < limit1; ++x) {
for (int y = 0; y < limit2; ++y) {
int temp = matrix[x][y];
matrix[x][y] = matrix[n - y - 1][x];
matrix[n - y - 1][x] = matrix[n - x - 1][n - y - 1];
matrix[n - x - 1][n - y - 1] = matrix[y][n - x - 1];
matrix[y][n - x - 1] = temp;
}
}
}
}107. 第50题. Pow(x, n)
参考题解:官方题解
题目:
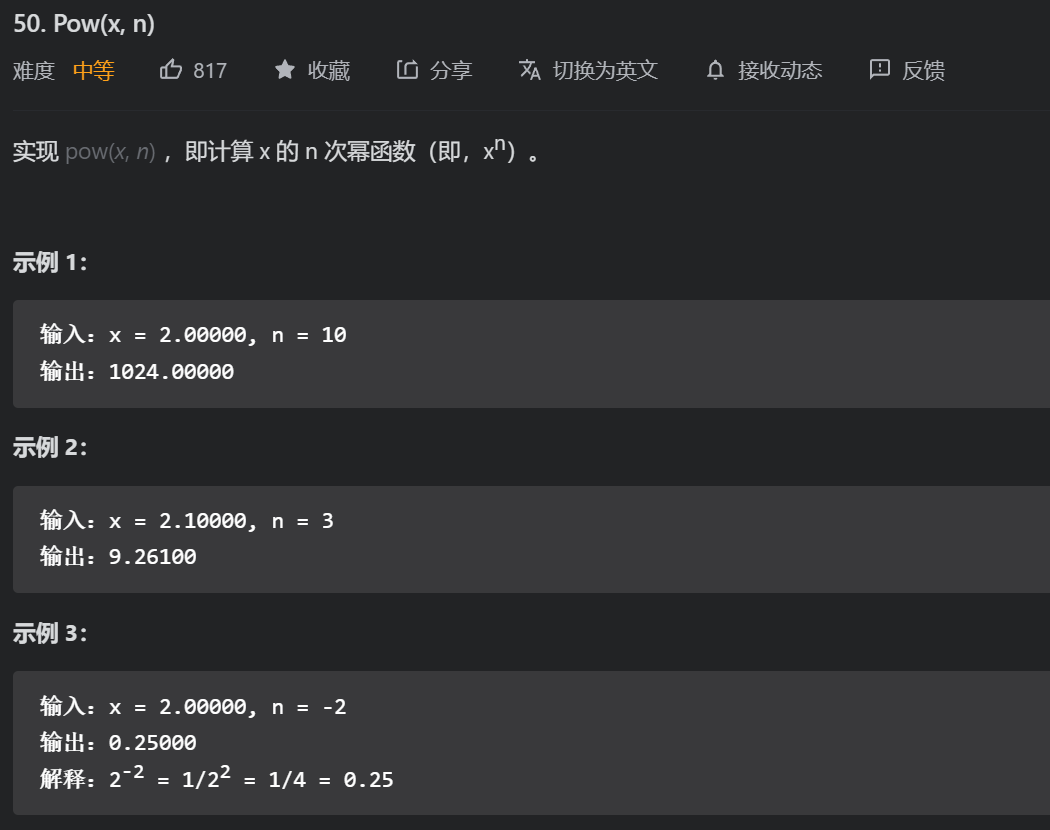
标签:
- 必考
- 反复错
思路:
题解:
class Solution {
public double myPow(double x, int n) {
long N = n;
return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
}
public double quickMul(double x, long N) {
if (N == 0) {
return 1.0;
}
double y = quickMul(x, N / 2);
return N % 2 == 0 ? y * y : y * y * x;
}
}108. 第475题. 供暖器
参考题解:官方题解
题目:
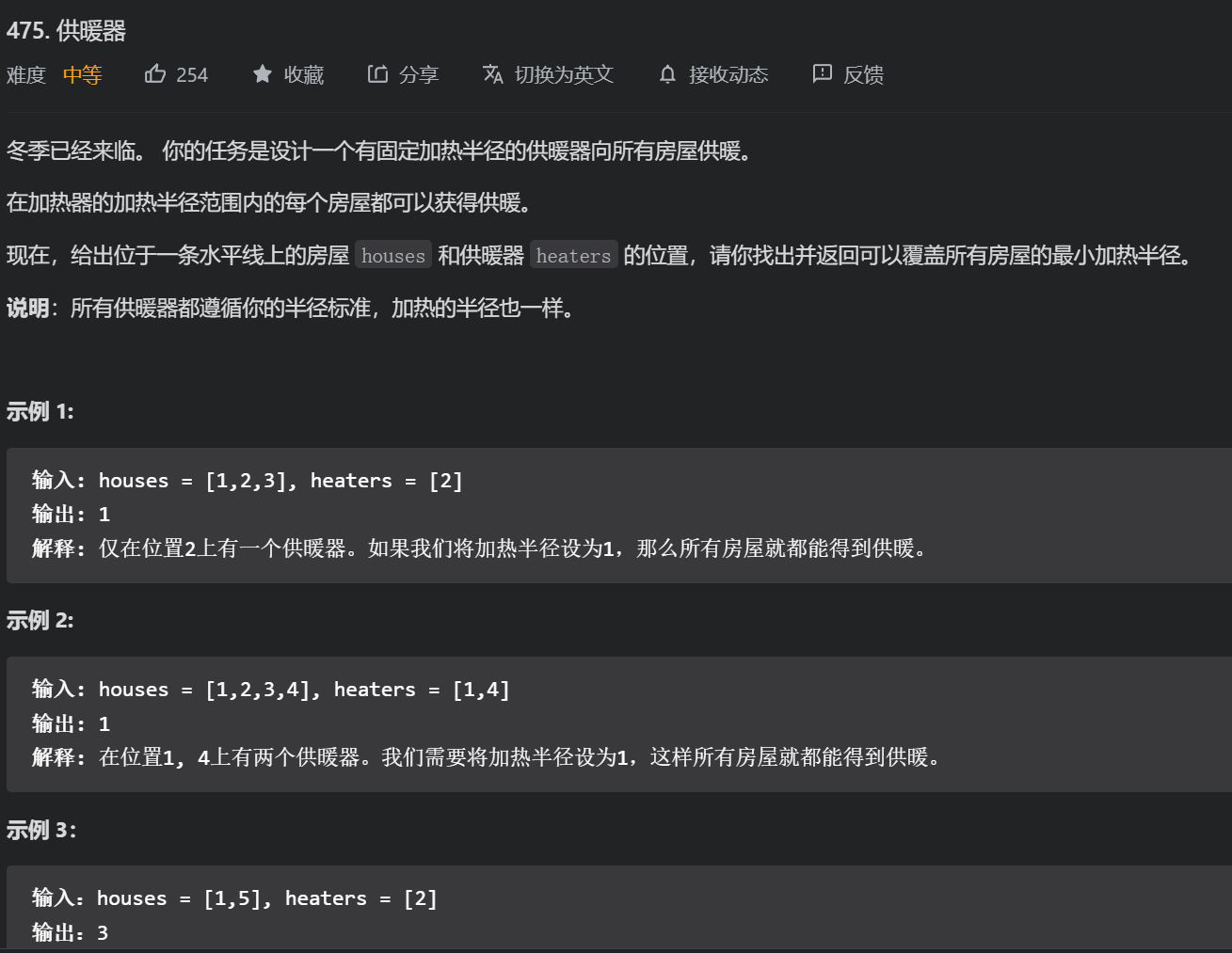
标签:
- 必考
- 双指针
思路:
- 首先对房屋和加热器进行排序。
- 随后,遍历房屋,内部再来一个 while 遍历。这里为什么要 while 呢?因为可能一次性不能挪到最后面!所以需要多次挪,每次 j++,再调整 curDistance。
- 最后,取最短半径里面的最大半径,就是结果。
- 这里面这个内部的 while 是思考的难点!
题解:
class Solution {
public int findRadius(int[] houses, int[] heaters) {
Arrays.sort(houses);
Arrays.sort(heaters);
int ans = 0;
for (int i = 0, j = 0; i < houses.length; i++) {
int curDistance = Math.abs(houses[i] - heaters[j]);
while (j < heaters.length - 1 && Math.abs(houses[i] - heaters[j]) >= Math.abs(houses[i] - heaters[j + 1])) {
j++;
curDistance = Math.min(curDistance, Math.abs(houses[i] - heaters[j]));
}
ans = Math.max(ans, curDistance);
}
return ans;
}
}




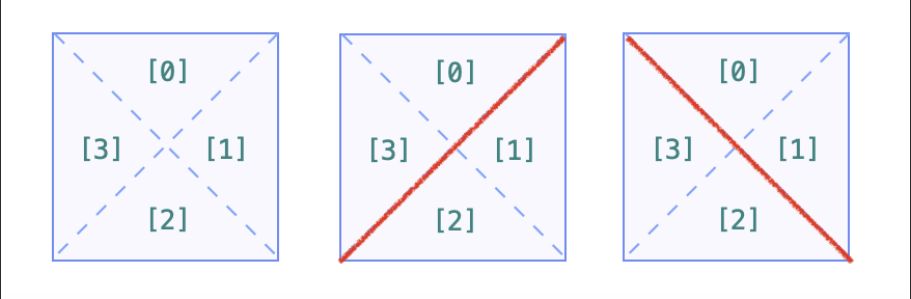
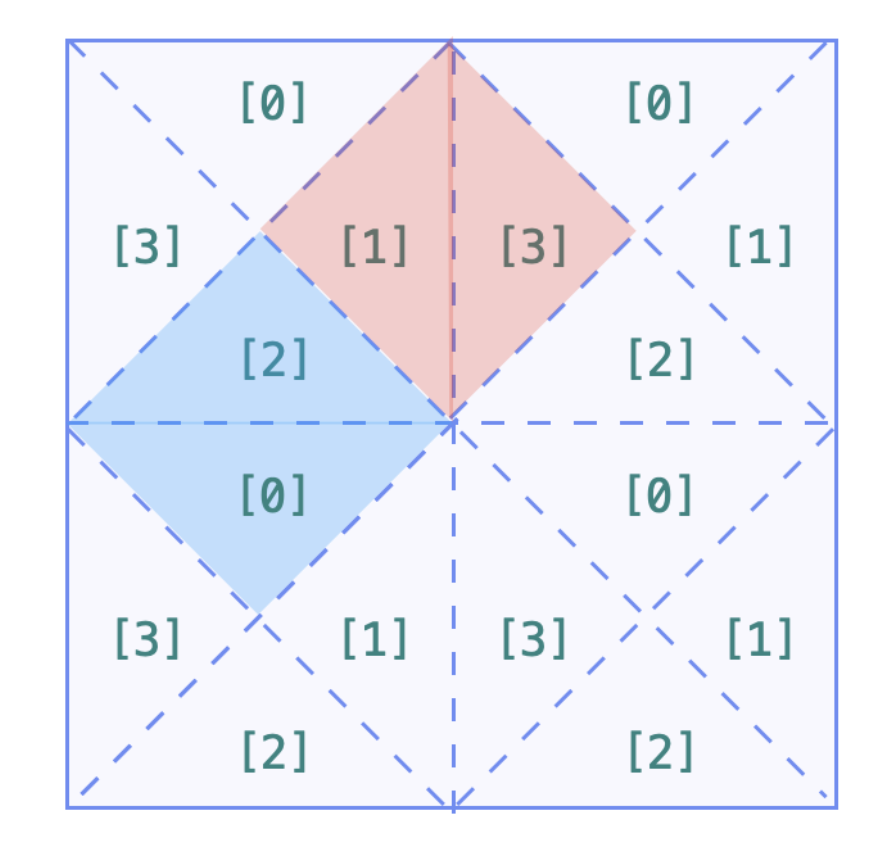
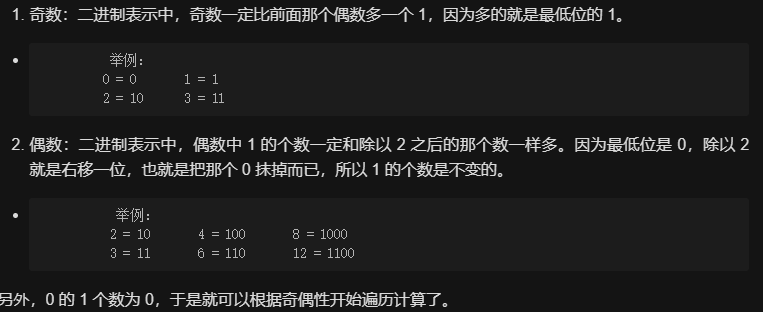

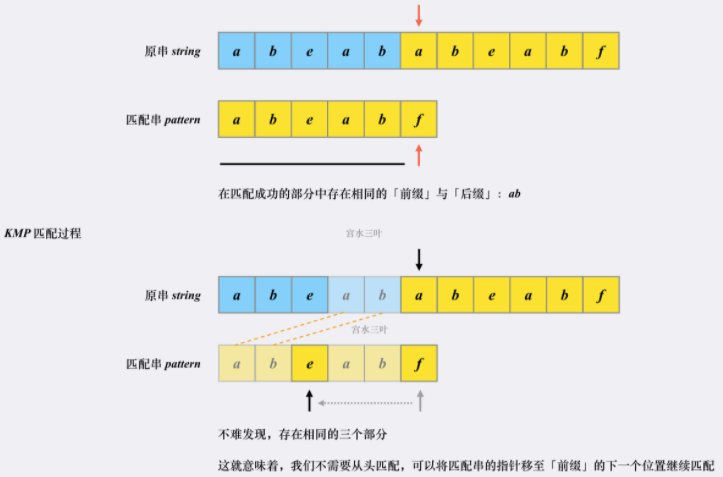
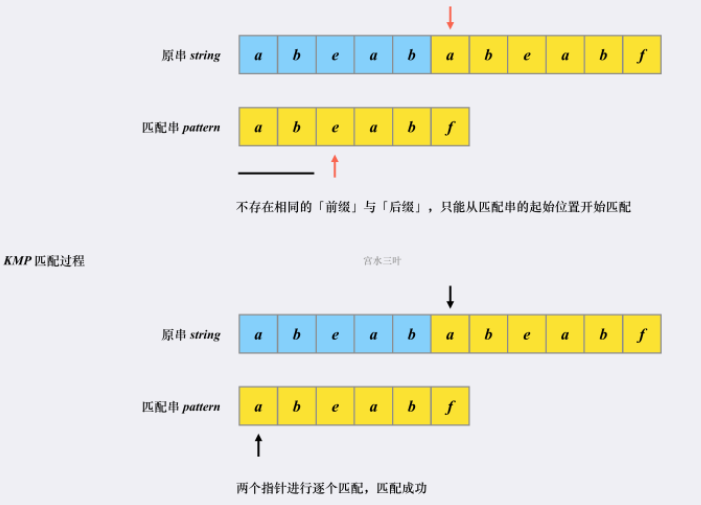
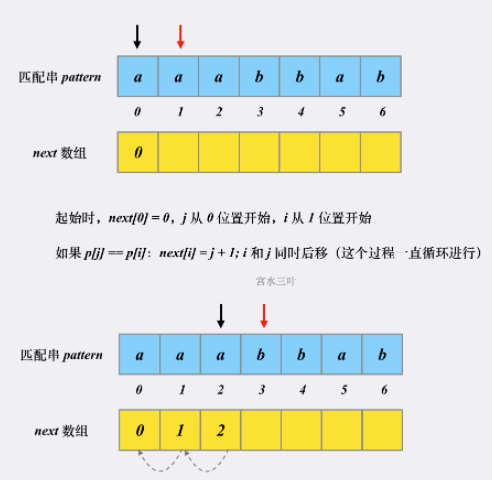
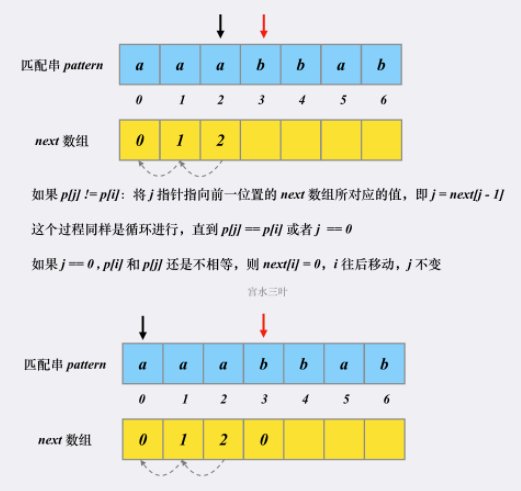
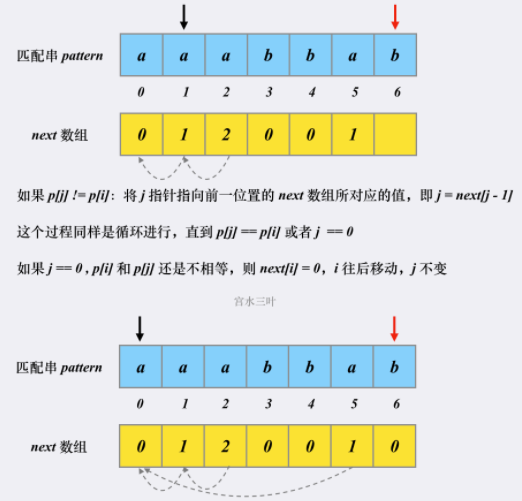


Comments | NOTHING