研一算法导论课程,为了加深自己对算法的理解,将算法导论内容整理于此。
第一部分 基础知识
1. 各种基础
各种定义
算法:通用性、有效性、确定性、有穷性。
数据结构:一种存储和组织数据的方式。
时间复杂度符号:Θ:渐进的给出函数的上界和下界。O:(只有)渐进上界。Ω:(只有)渐进下界。
其他时间复杂度符号:o:非紧的渐进上界,w:非紧的渐进下界。
时间复杂度计算法:代入法,递归树法,主方法。
伪随机数生成器:是一种确定性算法,返回的值统计上随机。
伪代码规则
样例1:
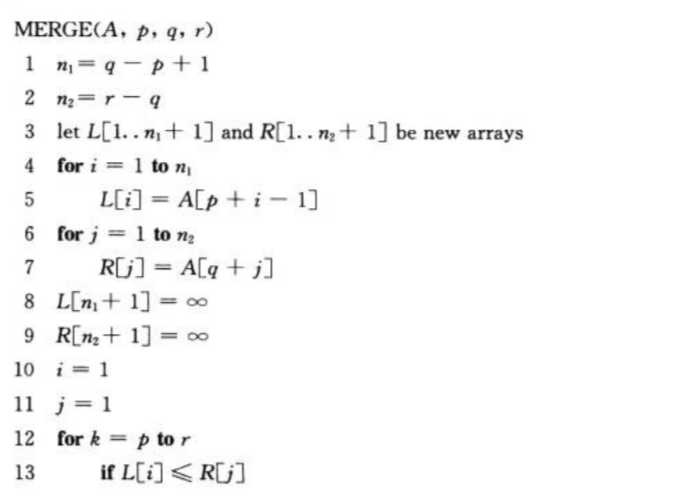
样例2:

2. 分治策略
分治思想
分治法求解问题:分解、解决、合并。其中,主函数负责分解和合并,子函数负责解决。
分治相关算法问题
最大子数组问题
- 问题实例:买股票
- 求解算法:分治法
- 求解思路:

- 函数:findMaximumSubarray主函数,findMaxCrossingSubarray子函数



3. 冒泡排序
4. 插入排序
插入排序算法:

图解:
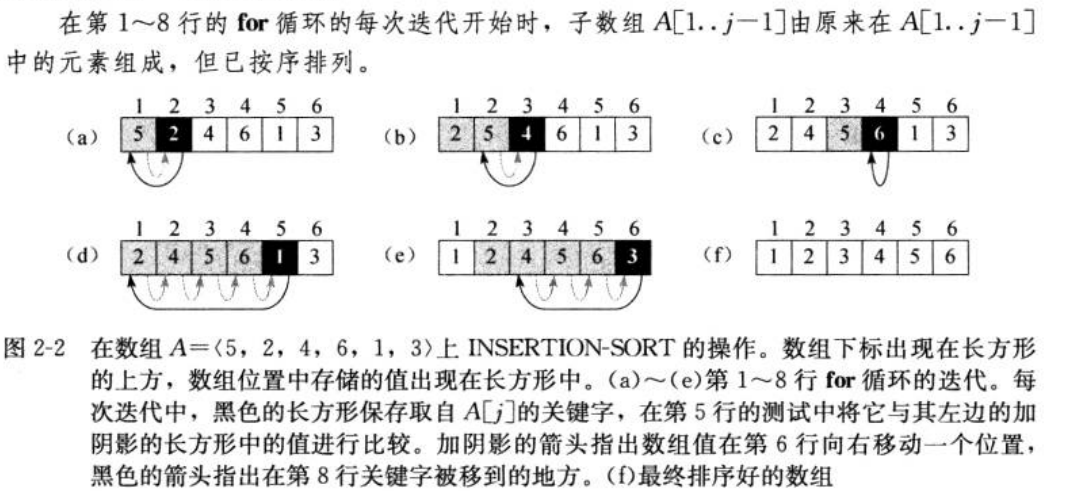
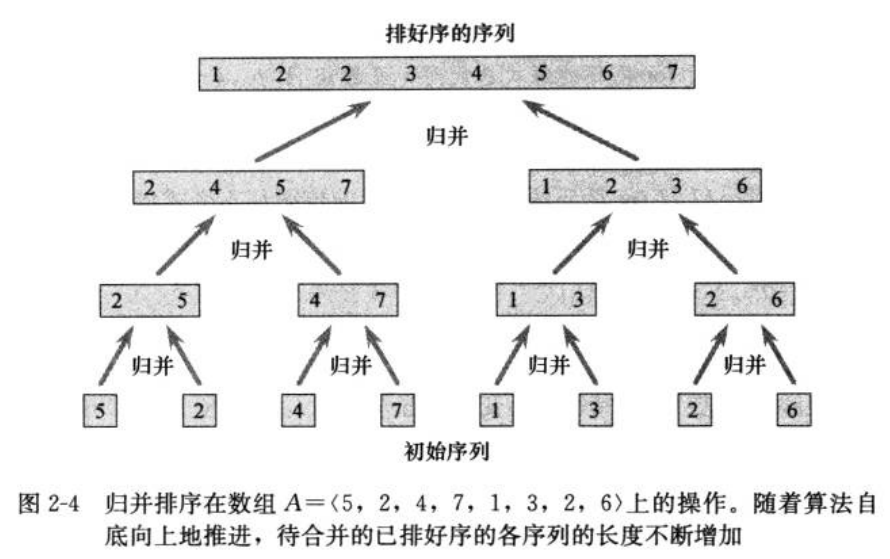
5. 归并排序
时间复杂度 O(n log n)
归并排序算法:主函数:mergeSort,子函数:merge

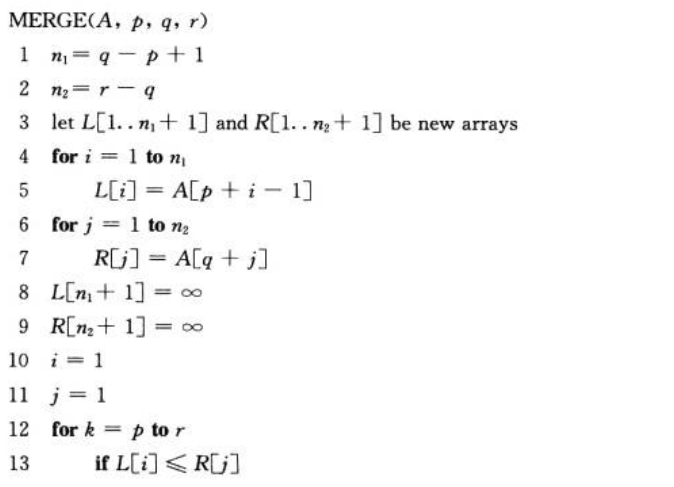
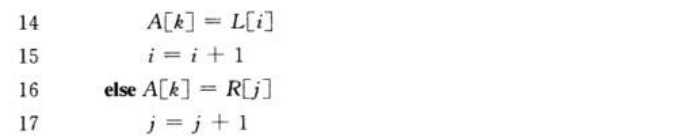
图解:
第二部分 排序和顺序统计量
1. 堆排序
堆排序相关内容
时间: O(n log n)
空间:有空间原址性,常数空间复杂度。
堆:近似的完全二叉树,所以又叫二叉堆。
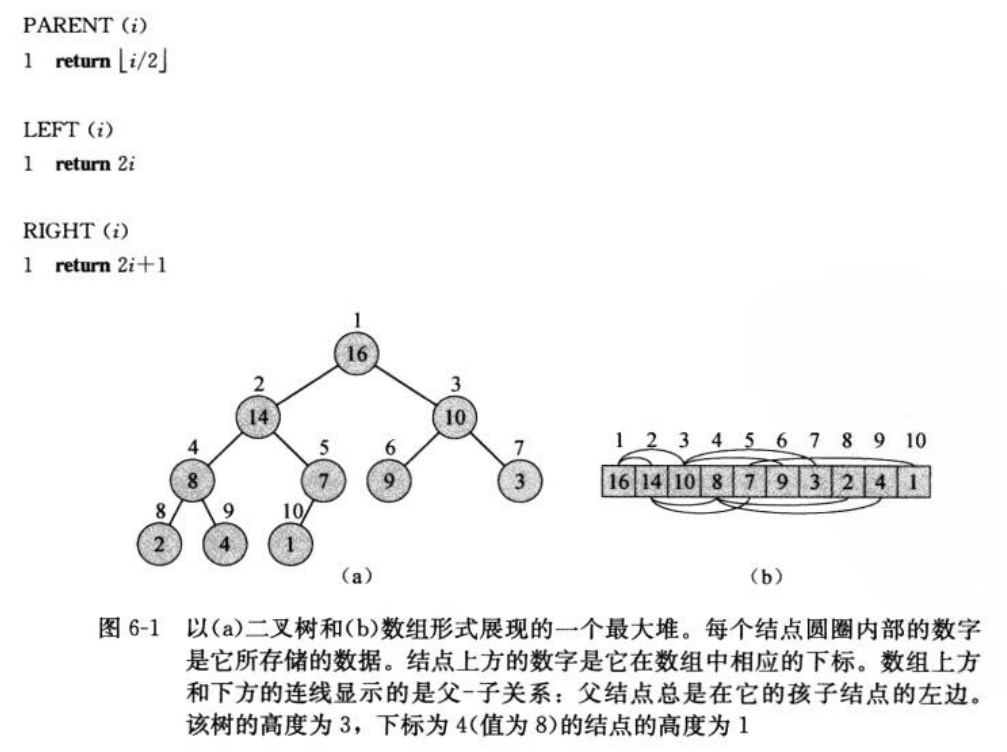
最大堆:除了根节点,其他节点都不大于父节点。最小堆反之。也就是最大最小是指根的性质是最大还是最小。最小堆常用于优先队列。
常用函数:维护最大堆 maxHeapify,构建最大堆 buildMaxHeap,堆排序 heapSort,构建优先队列 maxHeapInsert、heapExtractMax、heapIncreaseKey、heapMaximum。

maxHeapify 算法、图例及时间复杂度 O(h):

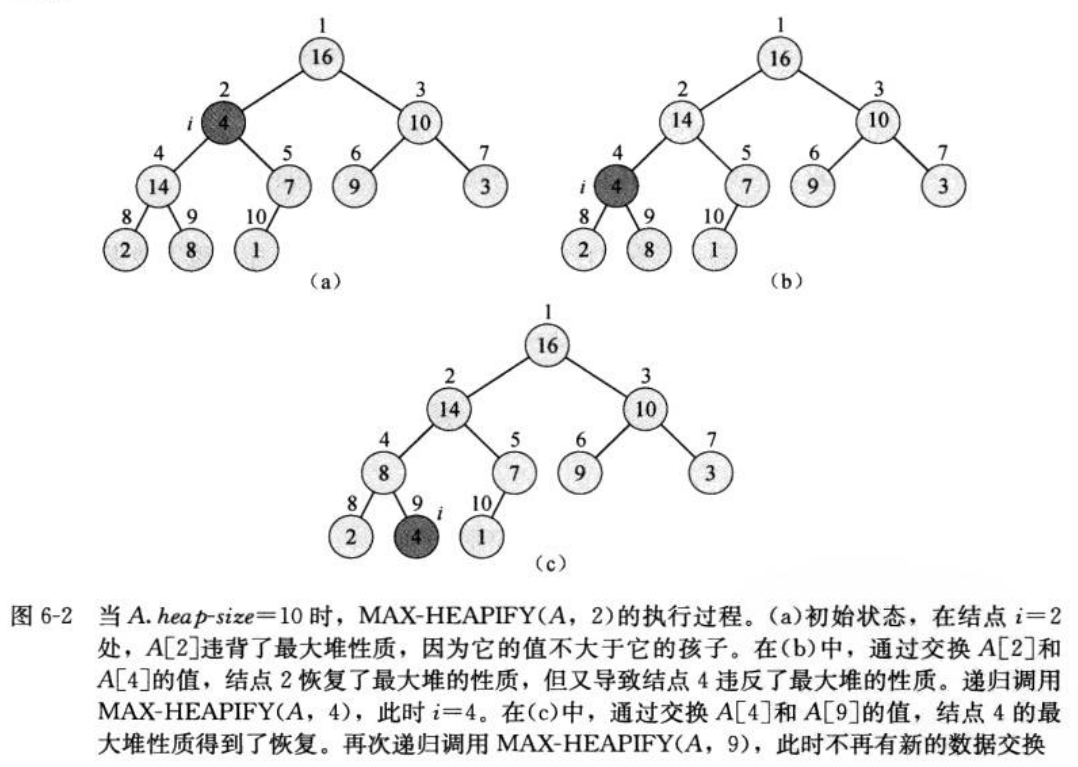
buildMaxHeap 算法、图例、时间复杂度 O(n):

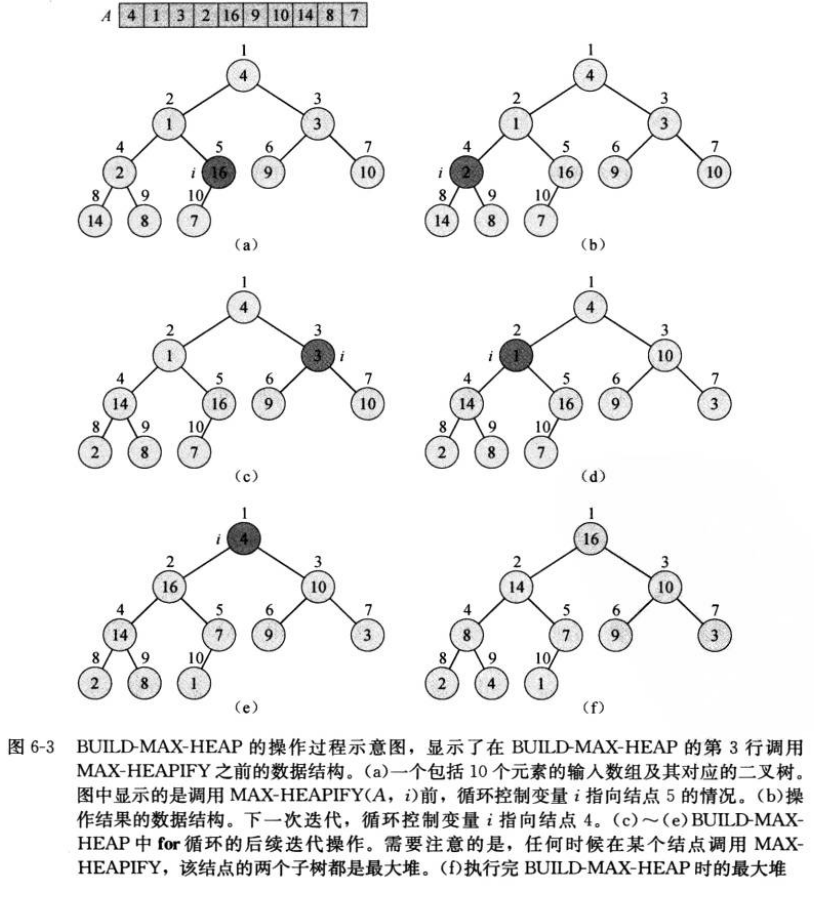
heapSort 算法、图例、时间复杂度 O(n log n):


优先队列相关内容
优先队列:

应用:操作系统作业调度,根据优先级排列作业调度顺序。
2. 快速排序
快速排序也采用了分治法思想。
时间:期望为 O(n log n),且常数项非常小,一般比堆排序还快。
快速排序算法:主函数:quickSort,子函数:partition
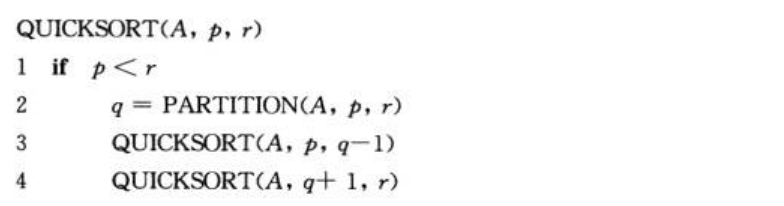

图解:

可以进行随机化改进子函数 partition:
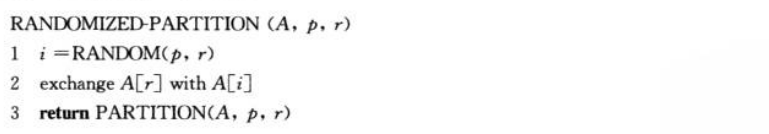
3. 线性时间排序
比较排序和线性时间排序
比较排序:元素次序依赖比较的排序。前面提到的排序都是线性时间排序。比较排序的时间下界为 Ω(n log n)。
线性时间排序:包括 计数排序、基数排序和桶排序,它们依赖计算而不是比较。它们的时间下界是 Ω(n)。
计数排序
计数排序用一个数组存储每种数的数量,最后排多少位直接计数就能算出。
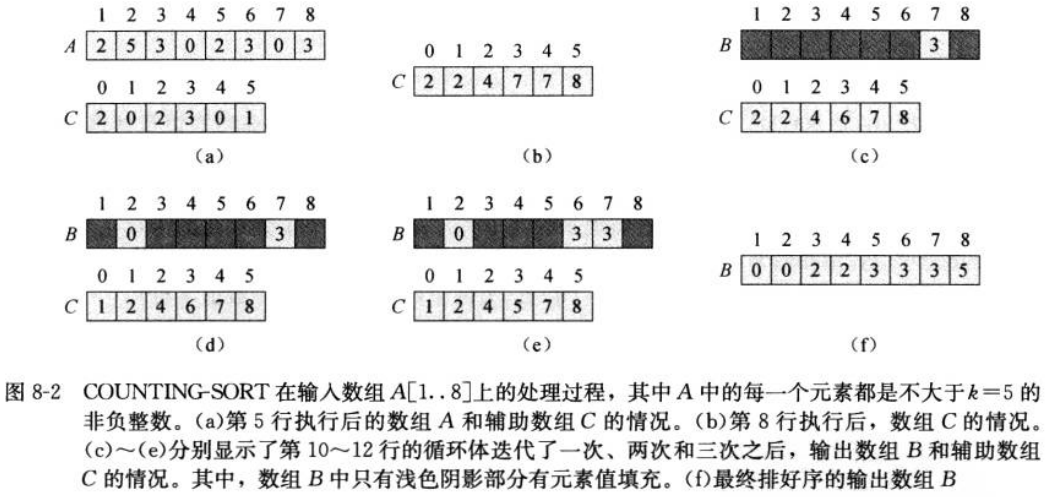
计数排序算法:

图解:
基数排序
基数排序从低位到高位,按照指定位排序。这也要求每次的排序都必须是稳定的排序算法。
基数排序算法:

图解:

桶排序
桶排序将区间划分为






Comments | NOTHING