论文:Beta Embeddings for Multi-Hop Logical Reasoning in Knowledge Graphs
NIPS 2020的一篇论文,涉及知识嵌入方法和Multi-Hop QA,有完整代码
- 作者:Hongyu Ren,Jure Leskovec
- pdf:https://arxiv.org/pdf/2010.11465.pdf
- github:https://github.com/snap-stanford/KGReasoning(包含三种模型,
BetaE,Query2box,GQE)
0. Abstract
为处理知识图谱存在的规模庞大和不完整问题,近期研究采用知识嵌入方法,将知识图谱实体嵌入到低维空间中,利用嵌入获取答案实体。当前研究条件下的知识嵌入存在的局限包括:
- 无法处理所有任意一阶逻辑查询(FOL),特别是无法处理否定运算
- 不能自然地模拟不确定性
文中提出的BetaE模型能处理所有一阶逻辑操作(与、或、非)。其核心思想是采用了带有界支持(bounded support)的概率分布,尤其是Beta概率分布,将问题及实体嵌入到概率分布中,从而模拟不确定性。逻辑操作在神经网络构造的概率嵌入空间中完成
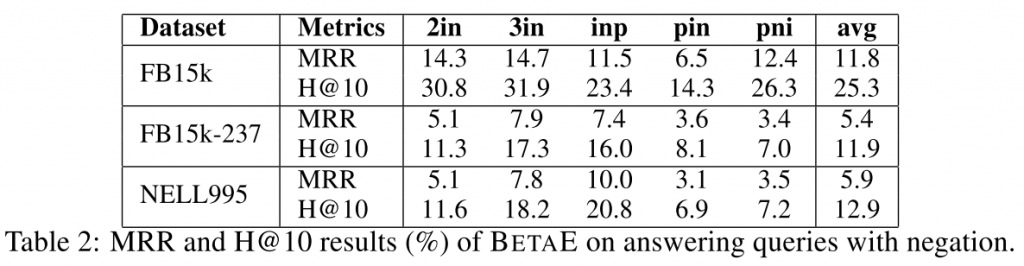
文中的BetaE模型在三个大型不完整知识图谱上均实现了最好成绩,比之前不支持否定运算的模型提高了25.4%
1. Introduction
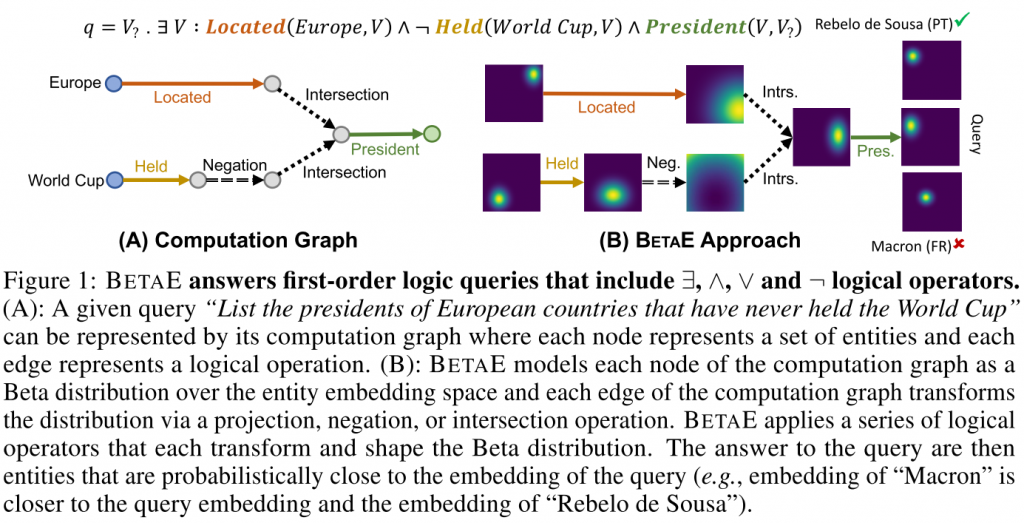
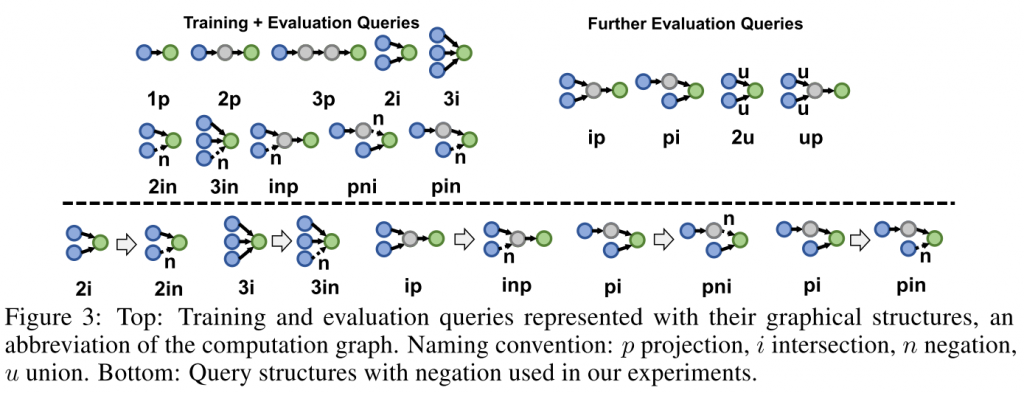
知识图谱中的推理涉及一阶逻辑查询first-order logic, FOL,包括:量化quantification,连接conjunction,析取disjunction,取反negation。相关例子如下图所示
当前的知识嵌入方法不支持取反negation操作,仅支持正一阶查询existential positive first-order, EPFO
本文贡献主要包括:
- 概率建模方法,可以反映查询的不确定性
- 通过基于β分布的神经网络模型,支持
FOL - 可以模拟实际操作,如取两次反等于正
- 支持任意
FOL查询(后两条有点凑数)
2. Related Work
知识图谱嵌入中的不确定性
当前知识嵌入方法,如KG2E和TransG,主要关注链路预测。本文作者认为这些方法不好应用在多跳推理任务中(实际上上一篇文章已经讲了,链路预测可以解决多跳推理问题)。本文的解决方案是,通过神经网络学习概率嵌入方法,实现对复杂查询问题的多跳推理
知识图谱多跳推理
相比于使用多跳规则或路径提高链路预测性能的方法,知识嵌入方法能够直接嵌入和回答复杂FOL查询,而不用对中间实体建模。这样提高了算法的可扩展性(不随知识图谱扩大而变慢)
3. Preliminaries

- 计算图:一种异构树,叶节点表示锚节点
anchor entity(?),根节点表示答案实体集合。对给定的FOL查询,通过跟踪计算图并执行逻辑算子,最后观察根节点中的实体集合获取答案。这种计算过程类似于遍历知识图谱。基本运算包括以下三种:关系投影、交、非(并可以被交和非的联合运算代替)

4. Probabilistic Embeddings for Logical Reasoning
4.1 实体和查询的β嵌入
嵌入的目标包括:
其中,闭包的逻辑算子有两点作用:
β分布包含两个形状参数α和β,β分布的重要性质是概率分布函数PDF,β分布的不确定性可以通过微分熵H反映

令每个实体都有β分布,对应概率分布为pS
4.2 概率逻辑算子
三种概率逻辑算子,可以将一或多个β嵌入转换为一个新的β嵌入
概率投影算子
采用多层感知机模型,针对不同关系r训练一一对应的模型。结果嵌入S'是固定大小的嵌入向量

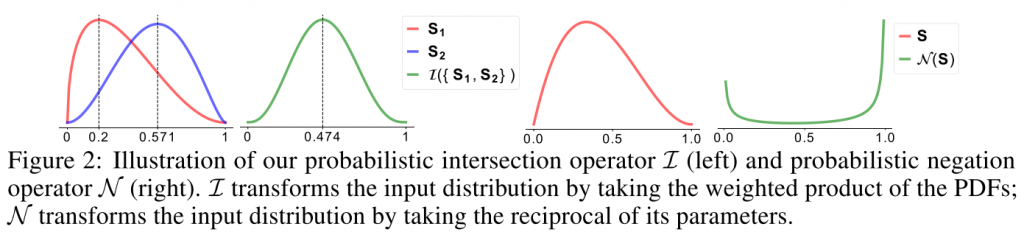
概率交集算子
输出嵌入向量是输入嵌入的归一化求和,也就是z = 1/n
为了交集算子有更强的表现能力,对(2)内的每个输入嵌入,引入了注意力机制(3)、(4)。其中注意力标量的计算是通过多层感知机进行计算


- (2):输出嵌入的计算方式,是对所有注意力输入嵌入的归一化求和
- (3):注意力标量计算方法
- (4):注意力输入嵌入计算方法,融合了β分布
概率补集算子
补集计算方法就是将β分布的α和β取倒数。这种方法满足补集的补集是原集的要求
4.3 学习β嵌入
距离
输入是n维β实体和查询嵌入,则每个输入都有n个β分布和2n个参数
计算实体和查询的距离,方法是计算两个β嵌入的各个维度的KL散度之和
- (5):计算实体嵌入和查询嵌入的距离。这里是先
v后q,论文里介绍说,这样查询嵌入会覆盖所有答案实体嵌入的模式(?)
训练目标
训练目标是最小化查询嵌入和答案实体嵌入的距离,同时,通过负采样,最大化查询嵌入和其他实体嵌入的距离
- (6):损失函数,其中k是超参数,是随机选取负样本的个数
求并集
模型对求并集有一定限制。作者的另一模型,Q2B,实现了对求并集的改进
5. Experiments
5.1 实验配置
- 数据集:FB15k、FB15k-237、NELL995,同时根据作者的另一篇文章进行预处理
- 评价方案:考察的主要是缺少查询路径的实体
non-trivial answer。求出每个实体的距离,进行排名,从而获取平均倒数秩Mean Reciprocal Rank, MRR(排名的倒数),以及获取另一个评价指标是Hits at K, H@K(排名前k个例子中多少是正确分类的) - 查询:同样是基于另一篇文章的9种查询结构,并提供了2种改进结构。包括5种联合结构
1p 2p 3p 2i 3i,5种带否定的新结构2in 3in inp pni pin。为了评估模型的泛化能力,还提供了训练时没有的新型逻辑结构ip pi 2u up进行评价。
5.2 模拟任意FOL查询
EPFO建模查询
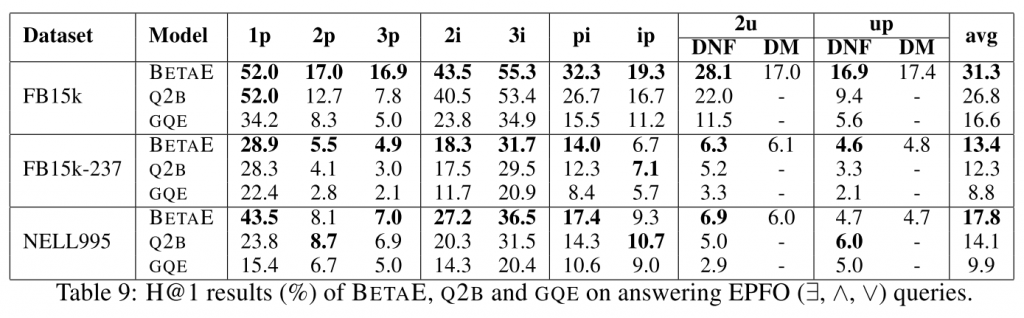
由于Q2B和GQE都不能进行否定形式建模,因此用EPFO建模进行比较



DNF和DM
DNF是正常形式,DM是基于德摩根律转换的有否定和联合的形式。DM更难一些,而BetaE仍然取得了一定效果
否定建模查询

5.3 查询的不确定性建模
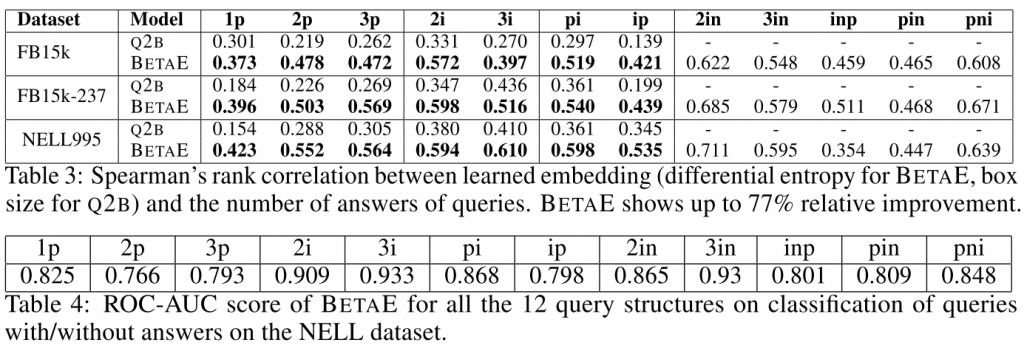
为衡量BetaE的查询不确定性评估能力,采用两种评价方法:Spearman秩相关系数Spearman's rank correlation coefficient, SRCC和Pearson相关系数Pearson's correlation coefficient, PCC。其中SRCC用于衡量变量排序的统计依赖性,PCC衡量变量的线性相关性。与Q2B进行对比,结果提高很大
无答案查询建模
由于BetaE可以对查询的不确定性建模,因此可以用查询嵌入的微分熵判断查询结构是否为空。计算微分熵并用其进行分类判断是否有答案,评价指标是AUC。结果显示,可以判断是否没有答案

6. Conclusion
本文提出的BetaE模型是第一个能够处理知识图谱上任意FOL查询的知识嵌入方法。BetaE可以通过可扩展的方式跟踪计算图,使用概率逻辑算子将查询嵌入到β分布中,进行多跳推理。实验证明,BetaE回答任意逻辑查询和不确定性建模方面明显优于过去的最先进技术
论文分析
对过程介绍的很详细,是篇知识嵌入小白也能安心阅读的好论文。效果提升很大,相对于以往的嵌入方法应该是有质的飞跃,可以继续探索





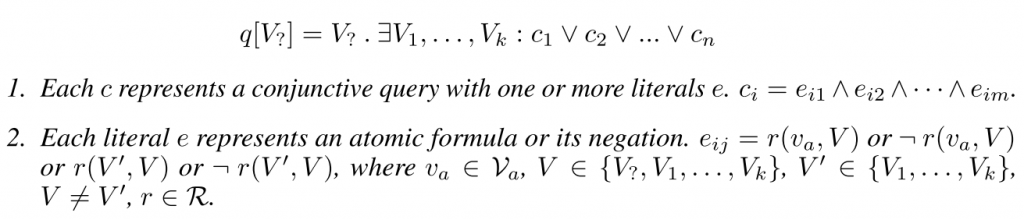



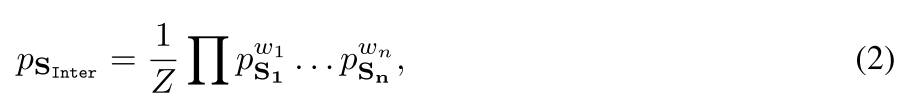
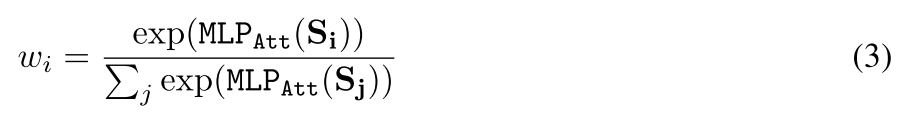
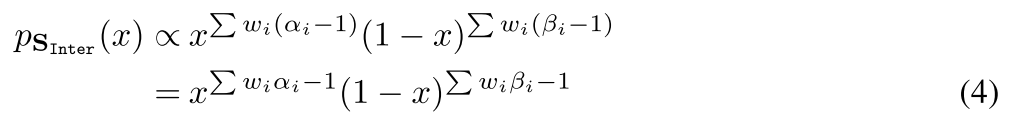
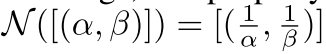








Comments | NOTHING